Het CBS heeft op 23 februari cijfers openbaar gemaakt, die ons in staat stelden de effectiviteit van de mRNA vaccins te berekenen. Die blijkt vrijwel nihil geweest te zijn, zoals blijkt uit deze cijfers. In dit artikel (in samenwerking met Hans Verwaart) leggen wij het uit. Dit artikel wordt ook geplaatst op LinkedIn. Het is voor de hand liggend dat dit artikel door sommige lezers van LinkedIn als onwelgevallig wordt beschouwd en zullen wellicht verzoeken dit te verwijderen. Daarom ook meteen maar een oproep om dit zoveel mogelijk te delen.
Op 23 februari 2024 publiceerde het CBS een artikel met de intentie aan te tonen dat het weglaten van de periode tot 2 weken na de tweede vaccinatie weinig verschil maakte in het sterftebeeld. Dit is het bewuste artikel: Covid-vaccinatiestatus en sterfte.
Wat is er eigenlijk aan de hand? Omdat de werkzaamheid van de vaccins pas 2 weken na het voltooien van de bassiserie op peil zou zijn, werd je pas gezien als “volledig gevaccineerd” na deze twee weken. Dat lijkt redelijk, maar toch heeft het CBS deze definitie nu bijgesteld. Maar wat laten de cijfers in dit rapport nog meer zien? Er was kritiek op deze aanpak, want er zouden juist in die weken na de 1e vaccinatie ook veel slachtoffers vallen. Dat zien we ook in de grafieken, maar het CBS besteedt er geen aandacht aan.
Dit is één van de grafieken uit Qatar die ons het nut vaccineren moest tonen:
Deze grafiek geeft de suggestie dat je vanaf week 2 voor 68% bent beschermd en na de tweede prik voor 95%. Maar is dat ook zo?

Zoals we straks zullen zien, lijkt er in de periode tussen de 1e en 2e vaccinatie (minstens 4 weken) geen enkele afname te zien in de sterfte aan covid-19. Een uitleg kan zijn dat het vaccin alleen sterfte kan voorkomen door een besmetting die plaats vindt nadat de bescherming op peil is. Sterfte vindt dan pas plaats enkele weken na de besmetting, dus met die uitleg is het verklaarbaar dat we in de eerste maand na de eerste prik geen enkel effect zien.
Over de noodzaak voor de tweede prik heeft de overheid ook gepubliceerd. In Vier redenen waarom je tweede coronaprik geen overbodige luxe is schreef de overheid dat de tweede prik gewenst was om meerdere redenen, waaronder “Zonder tweede prik neemt de basisbescherming van de eerste prik sneller af en is minder goed.” Dus die basisbescherming was er wel degelijk, maar nog niet optimaal, verwarrend. Ook zal een besmetting op de eerste dag van vaccinatie nog niet tegengehouden zijn door het vaccin. Maar een besmetting na een week toch wel voor het grootste deel. 95% bescherming was toegezegd, dus een verwachting van zeg 50% zou toch redelijk moeten zijn na de eerste vaccinatie? Als in alle redelijkheid gesteld zou worden dat toch de eerste 4 weken moeten worden uitgesloten voor debescherming, dan is dus alle daling van de coronasterfte toe te schrijven aan opbouw van natuurlijke immuniteit en vaccinatie mosterd na de maaltijd.
Het CBS heeft besloten de weken na de tweede vaccinatie nu toch mee te nemen als “volledig gevaccineerd” en is met een aanvullend rapport gekomen. Het wijzigen van deze definitie is voor dit artikel verder niet relevant, maar het beschikbaar komen van de tussentellingen juist wel. De conclusie van het CBS is vervolgens:
Het hanteren van een andere definitie voor vaccinatiestatus ‘gevaccineerd’, waarbij geen rekening wordt gehouden met de wachttijd na vaccinatie, resulteert in een vergelijkbaar sterftebeeld voor zowel overlijden aan COVID-19 als non-COVID-19 als wanneer de wachttijd wel wordt meegenomen.
Dat nemen we voor kennisgeving aan. Maar nu kunnen we wel uitzoeken wat de bescherming van het vaccin is in de periode tussen de eerste en tweede vaccinatie. De tabellen die CBS aanvoert, stellen ons in staat om exact te berekenen wat het effect was van de eerste prik, dus de kans op overlijden aan covid-19 tussen de eerste en de tweede prik. Personen die geen prik namen, blijven dus buiten beschouwing, dat is prettig.
Experimento
Als je zou willen weten wat de bescherming van het vaccin zou zijn, dan kun je daar een experiment voor opzetten. Je verdeelt de bevolking in twee groepen, waarvan je het ene deel wel en het andere deel niet vaccineert en je kijkt wat de verschillen zijn. Bij een perfect vaccin overlijdt er niemand meer aan covid-19 en bij een niet-werkend vaccin is er geen verschil.
Dat experiment is op kleine schaal en bij een selecte groep in de testfase al uitgevoerd en dat zou suggereren dat het vaccin een werkzaamheid zou hebben van mogelijk 95%. Maar nu de praktijk. Het experiment is daarna niet herhaald zonder selectie lijkt het, maar met het beschikbaar komen van de laatste CBS-cijfers, is het experiment toch gerealiseerd. We moeten er wel even voor gaan rekenen.
Jip en Janneke
Omdat het rekenen met de CBS-cijfers wat ingewikkeld lijkt, eerst in Jip en Janneke taal een uitleg met een voorbeeld.
Stel dat je wilt aantonen dat een vaccin een 100% werkzaamheid heeft. De gehele bevolking wordt gevaccineerd, verdeeld over 20 weken. Telkens 4 weken na de eerste prik geef je een tweede prik en we volgen het deel dat alleen een eerste prik heeft gekregen.
Van elk overlijden bekijken we wat de vaccinatie-status is en we tellen alleen de overlijdens die precies 1 prik hebben gehad. Dat is dus voortdurend 20% van de bevolking (4/20). Als de prik zijn werk goed doet, zal er in die groep niemand zitten die is overleden aan de ziekte waartegen het vaccin beschermt. Als het vaccin helemaal niets doet, dan vinden we in deze groep een aantal overlijdens dat ook 20% is van het totaal aantal overlijdens aan de ziekte. Als het aandeel 10% zou zijn, dan beschermt het vaccin dus voor 50%. Enzovoorts.
Omdat de sterftekans sterk afhangt van de leeftijd, vergelijken we niet met het aantal personen binnen de groep (hier dus 20%) maar met het totaal aantal overlijdens binnen de groep. Dit zal soms iets te hoge percentages opleveren en soms iets te laag, gemiddeld zal het weinig uitmaken. Als het vaccin 100% bescherming zou geven, maakt het al helemaal niets uit.
Deze afbeelding is een visualisatie van het concept.

We nemen aan dat elke 4 weken 20% van de overlijdens corona is (de rode poppetjes). Er kunnen soms wat minder (2) of meer (3) overlijdens zijn, maar de sterftekans voor corona is 20% in dit rekenvoorbeeld. Ook kunnen er 5 weken zitten tussen 1e en 2e prik (5), voor de kans maakt het niet uit. In (6) zien we de situatie als het vaccin een effectiviteit heeft van 50% vanaf de eerste dag. Als het vaccin pas vanaf week 3 een effectiviteit van 50% zou hebben, zien we de situatie (7) en meten we een VE van 25%. Alles fictief dus.
We zijn niet op zoek naar een exact percentage, maar een indicatie daarvoor. Als we dat wel willen weten, moeten we meer informatie hebben over de leeftijden bij overlijden. Die controle berekening hebben we gedaan, maar daarmee wordt de berekening te ingewikkeld voor dit artikel.
De tellingen
Het eenvoudigste deel van de analyse is het tellen van de verschillen in gevaccineerde overlijdens tussen de eerste en tweede prik. En dat doen we dan voor zowel de overlijdens aan covid-19 en de overige doodsoorzaken. In het CBS-rapport staan vier tabellen met aantallen overlijdens per week. Dit is een voorbeeld van een fragment uit deze tabellen:

Er zijn vier tabellen: twee voor overlijdens aan covid-19 en twee voor overlijdens aan overige oorzaken. Beide uitgesplitst naar wel of geen Wlz (=Wet langdurige zorg, wij zullen dit onderscheid niet maken). De tabellen gaan over de jaren 2021-2022, maar wij zullen alleen naar de cijfers tot juni 2021 gaan kijken, daarna zijn er nauwelijks nog eerste prikken, dus kunnen we daar niet meer vergelijken. Aangetekend moet ook worden dat een klein deel van de bevolking (naar schatting 7%) geen toestemming heeft gegeven voor registratie van de vaccinatiestatus in het CIMS-systeem. Daarvoor zullen we later corrigeren.
Bovendien was de sterfte aan covid-19 vanaf januari 2021 al sterk aan het afnemen, nog voordat de vaccins daaraan een bijdrage hadden kunnen leveren. Maar zeker kun je nog steeds een effect berekenen dat de vaccins zouden hebben gegeven bij het voorkomen van sterven aan covid-19.
Het CBS laat echter wel grafieken zien t/m eind 2022, waarschijnlijk om zo de suggestie te wekken dat het meenemen van de wachttijd weinig verschil maakt. Dit is een van deze 4 grafieken:

Er werden dus feitelijk gevaccineerde overledenen overgeheveld naar de groep no vacunado, waardoor er schijnbaar minder gevaccineerden overleden aan covid-19, maar ook aan andere oorzaken. Je zult daarvoor dus in elk geval moeten corrigeren.
De grafiek heeft de bedoeling te laten zien dat de 3 kolommen uit de tabel uiteindelijk tot dezelfde waar in 2022 komen, maar de informatie die we nodig hebben zit juist in het eerste deel, waar er een verschil zit tussen met en zonder wachttijd.
Omdat we middels dit rapport beschikken over beide aantallen (met en zonder wachttijd), kunnen we uitrekenen hoeveel mensen er meer (of minder) overleden gerelateerd aan de vaccinatie status.
Rekenwijze
De eerste stap is het per week berekenen van de sterfte tussen de 1e en 2e vaccinatie. Als we die groep beschouwen, zien we het effect van precies één vaccinatie. Dat aantal is het verschil tussen de aantallen in kolom 2 en 3. We weten nu dus hoeveel gevaccineerden er in elke week overleden aan zowel covid-19 als overige oorzaken, die exact 1 dosis hebben gekregen.
Deze cijfers gaan we nu vergelijken met alle overlijdens aan covid-19 en overige oorzaken in de betreffende weken. Laten we eerst naar de cijfers zelf kijken.

In deze grafiek is de totale sterfte aan covid-19 voor het gevaccineerde deel van de bevolking weergegeven als een groene lijn. Dat is kolom 2 uit het rapport. De rode lijn is het totaal aantal overlijdens aan covid-19 volgens de kwartaalrapportages van het CBS. We zien hier dat het aantal covid-19 overlijdens al vanaf januari sterk aan het dalen was, ruim voordat er werd gevaccineerd.
Door de stijgende vaccinatiegraad, stijgt uiteraard ook het aantal mensen dat ondanks de vaccinatie overleed aan covid-19, maar een deel van alle overlijdens zou wellicht voorkomen zijn door de vaccinatie. Daarvoor moeten we dus gaan rekenen.
Hoeveel vaccinaties?
De kunst is dus om te achterhalen hoe groot de in die 4 weken gevaccineerde groep was. Daarvoor kunnen we het deel van de totale gevaccineerde sterfte gebruiken tussen de 1e en 2e prik (de som van alle kolommen 2 min 3).
We gaan nu gebruik maken van het feit dat de leeftijdsverdeling bij de overlijdens aan covid-19 vrijwel dezelfde is als bij de totale cijfers. Dat hebben we al eerder aangetoond via een publicatie in ResearchGate.
Wat we dus doen is de verhouding bepalen tussen het totaal aantal overlijdens (alle oorzaken) van de eerste prikkers en het totaal aantal overlijdens dat het CBS via het RIVM rapporteert voor de betreffende week in de hele bevolking. Dat is dus het gevaccineerde deel van de bevolking. Die verhouding is onafhankelijk van de overlijdensoorzaak, maar wel inclusief het aantal overlijdens aan covid-19 zelf. Het percentage mensen dat één prik heeft gehad maar nog geen tweede schommelt daarmee rond de 15%-20%.
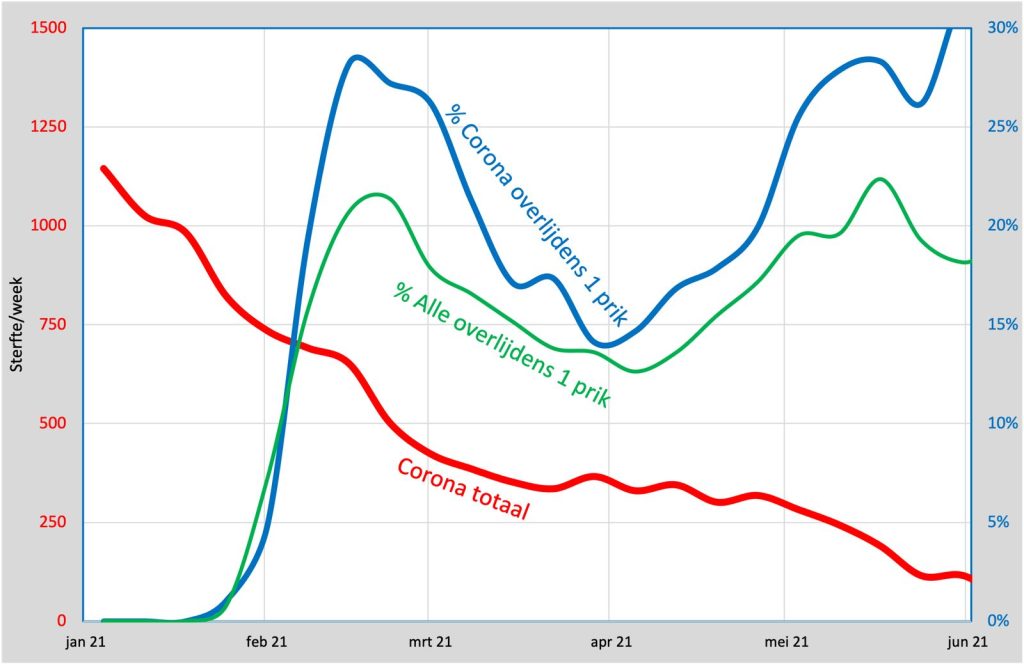
Diezelfde verhouding berekenen we ook voor de overlijdens aan covid-19. Uit de CBS-tabellen halen we weer het wekelijkse aantal overlijdens aan covid-19 tussen de 1e en 2e prik (kolom 3-2 voor alleen covid-19) en delen dat door het totaal aantal overlijdens aan covid-19 in die week. We corrigeren dit met 7% vanwege de genoemde onvolledige registratie in CIMS. De volgende grafiek brengt de beide percentages in beeld:
In deze grafiek is met een groene lijn het percentage van de gevaccineerden aangegeven dat tussen de 1e en 2e prik overleed. De blauwe lijn is het percentage overlijdens aan covid-19 tijdens diezelfde periode en dat zou dus lager moeten liggen dan het percentage bij de hele groep.
Tot onze verrassing ligt het percentage overlijdens aan covid-19 na vaccinatie vrijwel altijd hoger dan het verwachte percentage. Alleen in de eerste weken was dat iets lager, er werd toen met name zorgpersoneel gevaccineerd en daarvan overleed niemand. Er waren t/m mei in de wachtperiode 1251 overlijdens, terwijl de prognose uitkomt op 1001 overlijdens. Dat betekent dat de bescherming van de vaccins zelfs negatief uitkomt en wel -25%. En dat is een volstrekt ander percentage dan de 95% die ons in het vooruitzicht werd gesteld.
Vanaf eind mei neemt het aantal overlijdens aan covid-19 zo ver af dat de statistieken onbetrouwbaar worden. Het is juist die periode met nog maar lage sterfte aan covid-19 en hoge vaccinatiegraad die bij vele analyses aan zouden tonen dat de vaccins een goede bescherming gaven. Kleine verschillen in vaccinatiecijfers en doodsoorzaken geven een grote vertekening!
Bescherming in 2022
Nadat in 2021 twee besmettelijkere varianten verschenen (de Britse variant en de Delta) zou het reproductiegetal gestegen moeten zijn tot rond de 5. Daarvoor is een groepsimmuniteit nodig van tenminste 80%, die volgens de WHO alleen maar bereikt kan worden door vaccinatie. Omdat de covid-19 sterfte al in januari 2021 aan het dalen was, lijkt het of die immuniteit toch al bereikt was, nog voordat de vaccins werden uitgerold.
We hebben inmiddels inderdaad een vaccinatiegraad van rond de 84% en dat wordt door de politiek aangevoerd als oorzaak dat de pandemie succesvol zou zijn bestreden. Er zouden dan alleen nog maar ongevaccineerden overlijden aan covid-19.
Het CBS-rapport zou dat dus moeten laten zien. Echter, niets is minder waar! We hoeven alleen maar de overlijdens van de gevaccineerden bij elkaar op te tellen en die te vergelijken met het totaal aantal overlijdens dat het CBS rapporteert.
We tellen in het rapport 6518 gevaccineerden die aan covid-19 overleden, terwijl er in dat jaar in totaal 8432 overlijdens aan covid-19 werden geregistreerd. Rekening houdend met een vaccinatiegraad van 84% en 7% onderrapportage, komen we tot een VE van slechts 8%. Oftewel, de ongevaccineerde groep heeft een bescherming van tenminste 80% vanuit natuurlijke immuniteit en de gevaccineerde groep van 81,6%. Vaccineren geeft dus een extra bescherming van hooguit 1,6% voor een ziekte die al voor tenminste 95% verdwenen is.
Deze bescherming houdt nog geen rekening met het “Healthy vaccinee” effect, wat inhoudt dat gezonde mensen zich eerder laten vaccineren dan mensen met een slechte levensverwachting en dus eerder ongevaccineerd overlijden. Het is zeer waarschijnlijk dat zelfs die 1,6% daarmee ongedaan gemaakt wordt.
Ongewenste bijwerkingen
Dit is een apart verhaal en niet met zekerheid vast te stellen. Er is inmiddels een jaarlijkse oversterfte van rond de 15.000 die niet meer verklaard kunnen worden met de sterfte aan covid-19. Mocht blijken dat de vaccinatie hiervoor verantwoordelijk zou zijn, dan wordt daarmee ook direct de berekende VE-waarde beïnvloed en wel in negatieve zin. Dus de waarde die nu op 8% staat, zou daardoor ver onder de nul kunnen zakken. Deze analyse is een apart artikel waardig.
Hadden we dit al eerder kunnen weten?
Ja dat hadden we al in het voorjaar van 2021 kunnen weten. Elke epidemioloog weet dat vaccineren bijdraagt tot het verlagen van het reproductiegetal en wel in evenredigheid met de vaccinatiegraad. Dus als je de helft van de bevolking hebt gevaccineerd met een 100% effectief vaccin, moet het reproductiegetal ook zijn gehalveerd. In deze grafiek zou dan het effect van vaccinatie op de R-waarde te zien moeten zijn vanaf maart:
Het reproductiegetal is hier berekend op basis van de sterftecijfers. Het was in januari net rond de 0,95 en steeg zelfs nog iets tot 1,0. Maar we zien in maart geen enkele daling die het gevolg zou kunnen zijn van de vaccinaties! Door het seizoenseffect daalde het reproductiegetal pas in mei, zoals in deze grafiek is te zien.
De stippellijn is het veronderstelde verloop van de R-waarde als deze 95% effectief zou zijn geweest vanaf de tweede prik. We zien dat deze niet gevolgd werd en er dus geen noemenswaardig effect van de vaccinatie kan zijn geweest.
Conclusión
Door gebruik te maken van de cijfers in het rapport Covid-vaccinatiestatus en sterfte kunnen we de bescherming berekenen, die het vaccin ons gedurende de 4 weken na de eerste prik zou hebben gegeven. Die blijkt zelfs negatief uit te vallen: -12%. Dat betekent dus dat vaccinatie de kans om te overlijden gedurende de eerste 4 weken na vaccinatie zelfs verhoogd heeft.
Deze methode van berekenen geeft geen uitsluitsel hoe de bescherming geweest is in de daaropvolgende weken, maar het is niet aannemelijk dat er in die weken een duidelijke stijging geweest zou zijn die ook maar in de buurt van de beloofde 95% zou zitten.
Omdat het vaccin pas op zijn vroegst in maart bescherming heeft kunnen geven, is alle daling in covid-19 sterfte tot maart toe te schrijven aan de verdere opbouw van natuurlijke immuniteit, zoals ook bekend bij epidemiologen. Vaccinatie had de opbouw van immuniteit moeten versnellen, maar we zien juist een stagnatie. Alleen het openbaar maken van de volledige dataset met koppeling vaccinatiestatus-overlijden (kennelijk werkt het CBS daar wel mee) kan hierover duidelijkheid verschaffen.
De CBS-sterftecijfers voor 2022 laten zelfs zien dat de vaccins (vrijwel) geen enkele bescherming meer hebben gegeven. Toch heeft de minister besloten om ook voor 2024 weer een vaccinatiecampagne te gaan houden.
Ejemplo de cálculo
De berekeningen zijn vanuit het verhaal lastig te volgen, daarom een rekenvoorbeeld.
We gaan uit van week 10, dat is de week van 8 maart 2021. De cijfers komen dus uit Covid-vaccinatiestatus en sterfte, de totaalsterfte uit wat het CBS via het RIVM rapporteert en de sterfte aan corona uit de kwartaalrapportages van het CBS.
We nemen telkens de cijfers voor Wlz en nWlz samen. De sterfte tussen de 1e en 2e prik is dan (52-14) + (40-2) = 76 overlijdens aan covid-19 en (52-14) + (40-2) + (566-351) + (264-18) = 537 totaal overlijdens met 1 vaccinatie.
Het totaal aantal overlijdens in week 10 is 3245 en het aantal overlijdens binnen de 1 maal gevaccineerde groep in die week was 537, oftewel 537/3245 = 16,6%.
Volgens het CBS overleden er in die week 423 mensen aan covid-19, wat gevaccineerd zonder effect van vaccinatie 0,1655 X 423 = 70 overlijdens zou gaan geven. We nemen aan dat 7% van de gevaccineerden zich niet heeft laten registreren (dat getal zijn we een aantal maal tegengekomen) dus is de verwachte waarde voor het aantal overlijdens in week 10 dat eenmaal gevaccineerd was 65. Het percentage 1 maal gevaccineerd overleden aan covid-19 is dus 65/423 = 19,3%.

Ik begrijp het nog niet helemaal. Misschien kunnen jullie mijn vraag beantwoorden.
Op de CBS site staat het volgende:
Quote
‘Vaccinatiestatus ‘gevaccineerd’ is gedefinieerd als ‘volledig gevaccineerd’ (d.w.z. twee weken na twee goedgekeurde vaccinaties, of een positieve test minimaal 56 dagen voor minimaal één goedgekeurde vaccinatie, of vier weken na vaccinatie waarbij volgens het vaccinatiebewijs één vaccinatie als volledig gevaccineerd telt, of wanneer er een booster of herhaalprik is gezet zonder bekende basisserie) mogelijk met boosters en herhaalprikken. Vaccinatiestatus ‘ongevaccineerd’ is gedefinieerd als geen vaccinatie bekend of slechts één vaccinatie bekend zonder eerder gemelde besmetting (met uitzondering van het vaccin waarbij één vaccinatie als volledig gevaccineerd telde).
Unquote
Mijn vraag: Mensen met 1 ‘vaccinatie’ worden dus als ongevaccineerd beschouwd volgens de CBS methode. Pas bij een 2de prik (besmettingen even daargelaten) wordt het stempel ‘gevaccineerd’ gezet. Het enige dat veranderd is, is de periode daarna. Dan missen jullie toch mensen die na de eerste injectie zijn overleden en dus nooit aan een tweede zijn toegekomen? Of staat die informatie wel in de CBS tabellen?
Dit gaat dan even alleen over de prikken die 2 maal toegediend moesten worden. De mRNA prikken in principe. AZ was een eenmalige.
Het antwoord zit denk ik hierin (Herman is even offline):
“Zoals we straks zullen zien, lijkt er in de periode tussen de 1e en 2e vaccinatie (minstens 4 weken) geen enkele afname te zien in de sterfte aan covid-19. Een uitleg kan zijn dat het vaccin alleen sterfte kan voorkomen door een besmetting die plaats vindt nadat de bescherming op peil is. Sterfte vindt dan pas plaats enkele weken na de besmetting, dus met die uitleg is het verklaarbaar dat we in de eerste maand na de eerste prik geen enkel effect zien.”
(Dat geldt ook voor die twee weken ‘net geprikt’ daarna, denk ik dan.)
Er is nog iets. Ik heb op twitter de CSV bekeken die de basis is. Hier een willekeurig aantal regels:
2022,46,2022-11-20,33,243,059,427,8,707,0,17,T,T,fully vaccinated with delay
2022,47,2022-11-27,22,215,025,404,4,529,0,14,T,T,fully vaccinated with delay
2022,48,2022-12-04,43,362,089,634,5,559,0,14,T,T,fully vaccinated with delay
2022,49,2022-12-11,42,431,124,737,10,1693,0,36,T,T,fully vaccinated with delay
2022,50,2022-12-18,55,504,195,812,7,1007,0,23,T,T,fully vaccinated with delay
2022,51,2022-12-25,80,1017,532,1503,12,1169,0,25,T,T,fully vaccinated with delay
2022,52,2023-01-01,70,519,25,788,14,1168,0,24,T,T,fully vaccinated with delay
2021,1,2021-01-10,0,0,0,0,636,4838,3933,5742,T,T,immediately after first dose
2021,2,2021-01-17,0,0,0,0,597,4784,3844,5725,T,T,immediately after first dose
2021,3,2021-01-24,0,0,0,0,591,4375,3501,5248,T,T,immediately after first dose
2021,4,2021-01-31,8,1985,0,44,468,4253,3306,52,T,T,immediately after first dose
2021,5,2021-02-07,32,1266,259,2273,378,4234,3199,527,T,T,immediately after first dose
2021,6,2021-02-14,109,2241,1212,327,281,4474,3266,5682,T,T,immediately after first dose
2021,7,2021-02-21,155,2644,1492,3796,194,2784,1878,369,T,T,immediately after first dose
2021,8,2021-02-28,107,1471,717,2225,115,1712,985,244,T,T,immediately after first dose
2021,9,2021-03-07,72,935,366,1505,92,1598,867,2329,T,T,immediately after first dose
2021,10,2021-03-14,52,493,141,845,77,177,928,2611,T,T,immediately after first dose
2021,11,2021-03-21,27,288,0,6,67,2702,1375,4029,T,T,immediately after first dose
2021,12,2021-03-28,39,267,092,441,47,1044,486,1602,T,T,immediately after first dose
2021,13,2021-04-04,14,151,0,3,43,1959,822,3096,T,T,immediately after first dose
2021,14,2021-04-11,17,141,013,269,38,1769,582,2956,T,T,immediately after first dose
2021,15,2021-04-18,21,223,0,4,35,16,507,2692,T,T,immediately after first dose
2021,16,2021-04-25,11,064,0,1,27,1509,294,2723,T,T,immediately after first dose
2021,17,2021-05-02,15,174,0,3,37,1339,334,2344,T,T,immediately after first dose
2021,18,2021-05-09,21,21,0,4,24,1243,255,223,T,T,immediately after first dose
2021,19,2021-05-16,17,194,009,379,25,2133,546,372,T,T,immediately after first dose
2021,20,2021-05-23,16,183,0,4,15,1181,0,24,T,T,immediately after first dose
2021,21,2021-05-30,4,086,0,2,10,508,0,11,T,T,immediately after first dose
Een omschrijving is dus ‘immediately after first dose’. Ik wil graag de onderliggende data begrijpen. Deze kreet lijkt aan te geven dat het CBS misschien meer heeft gedeeld dan de bedoeling was?
Fuente: https://pastebin.com/raw/RvG4gyve
“Maar wat laten de cijfers in dit rapport nog meer zien? Er was kritiek op deze aanpak, want er zouden juist in die weken na de 1e vaccinatie ook veel slachtoffers vallen. Dat zien we ook in de grafieken, maar het CBS besteedt er geen aandacht aan.”
Dat is wat jij bedoelt denk ik.
AZ Vaxzevria was ook een dubbele dosis. Geen mRNA maar adenovector simian vaccin, met stukje van resus(makaak)aapjes erin. https://www.cbg-meb.nl/onderwerpen/medicijninformatie-vaccinaties/coronavaccins/covid-19-vaccin-astrazeneca
Ik zie het nu. Ze hebben het wel meegenomen. ‘zonder wachttijd, na eerste vaccinatie’. Dat is denk ik de categorie ‘immediately after first dose’.
Misschien een suggestie om een korte omschrijving van de onderliggende data toe te voegen aan de inleiding? Voor mij was het in ieder geval niet helemaal duidelijk. Nu wel.
Ga ervan uit dat dit artikel van alle kanten onder vuur wordt genomen. Dus maar beter om alles helder op te lijnen.
Ik vraag me af of CBS bewust het aantal overledenen na eerste vaccinatie heeft gepubliceerd, of was het een foutje? Vrij dodelijke fout (pardon the pun).
Er zijn ook internationaal al veel mensen in de data gedoken. Dit is niet meer terug te draaien.
Nu stop ik. Bedankt voor deze analyse weer.
Nog een aanvulling op de uitleg van Anton: het CBS maakt verwarrend onderscheid tussen “gevaccineerd” en “volledig gevaccineerd”. Gevaccineerd was 2 weken na de eerste prik, volledig gevaccineerd was je 2 weken na de 2e prik (of 4 weken na de 1e als er maar 1 prik was). Nu is het zo dat je volledig bent gevaccineerd direct na de 2e prik.
Maar voor de analyse maakt het veranderen van de definitie helemaal niets uit. Wel heeft het CBS als “service” gemeend te laten zien dat veranderen van de definitie weinig verschil maakt door de tussentellingen te publiceren. En die kunnen we nu dus nuttig gebruiken.
Ik sluit niet uit dat het CBS zich in het nauw gedreven voelde en met deze publicatie een boodschap afgegeven hebben die eigenlijk verboden was.
Ze zitten in drijfzand. Ze zakken steeds dieper weg. En als ze bewegen om er iets aan te willen doen wordt het alleen maar erger. Alleen van buiten afmaken soelaas geboden worden. Maar ja, dan moeten ze wel om hulp vragen. Zoals het er nu naar uitziet verzuipen ze liever … en zijn daarbij zelfs bereid de hele goegemeente mee te sleuren. Stelletje droeftoeters.
Wat ik geheel niet begrijp m.b.t. de effectiviteit van het vaccin is het feit dat eind 2021 begin 2022 de ziekenhuizen overvol lagen met coronapatiënten. In sommige landen Canada, Denemarken, Cyprus, Japan, Australië, Israël enz…. lagen er meer coronapatiënten dan ooit voorheen. Het vaccin zou ziekenhuisopname en sterfte voorkomen. Wanneer ik de cijfers van Our World in Data aanhaal, krijg ik te horen dat ik moet rekening houden met het aantal niet gevaccineerden en de cijfers in de juiste context moet plaatsen. Ik ben de mening toegedaan dat het vaccin helemaal geen ziekenhuisopname voorkomt, in het bijzonder omdat een deel van de ongevaccineerden door besmetting ook immuniteit opgebouwd zullen hebben. Is mijn denkwijze fout of moet ik vooraleer conclusies te trekken met een aantal bijkomende factoren rekening houden ? Alvast dank voor jullie reactie.
Dat zijn ook onze gedachten. Je ziet het ook vanaf februari 2021. Ziekenhuisopnames begonnen te stijgen op het moment dat er werd gevaccineerd
In aanvulling: de reden dat al die mensen als ongevaccineerd zijn opgenomen wordt veroorzaakt door het grootste Covid rookgordijn, ook hierboven genoemd; Het feit dat mensen pas als gevaccineerd worden gezien 2 weken na de 2de prik. Dit is wereldwijd toegepast. Zoals professor Norman Fenton ook al heeft aangegeven: op deze manier kun je het grootste vergif safe and effective laten lijken. Immers, iedereen die er binnen 6 weken aan overlijdt of er ziek van wordt, wordt als ongevaccinneerd beschouwd. De oplossing? Nog meer vaccineren natuurlijk. Een vicieuze cirkel.
Ik denk niet dat de kritiekloze narratief volgers dit weten. Dit ondanks het feit dat het gewoon op de RIVM site staat (of stond).
Dit simpele, niet ter discussie staande feit zou bij iedereen bekend moeten zijn.
Dit artikel is een gemiste kans.
Hierin wordt namelijk dezelfde fout gemaakt als bij de analyses van RIVM over de start van de vaccinaties: er kan met eenvoudige statistische technieken niets gezegd worden over de werkzaamheid van de vaccinatie omdat er veel te veel storende factoren zijn.
De definitie van gevaccineerd/ ongevaccineerd is slechts één van die storende factoren. Andere factoren zijn: neergaande trend epidemie na piek eind 2020, volgorde van vaccineren op basis van kwetsbaarheid/ leeftijdsgroepen, seizoenseffecten en speciale effecten als het ‘healthy vaccinee’ effect. Al dat soort effecten moet je eerst uit de sterftecijfers filteren, of de analyse meer specifiek maken (bv. per leeftijdsklasse) om werkelijk tot uitspraken te komen over de werkzaamheid van vaccins in de periode tot aan juni 2021. Alle sterftegevallen in deze periode op een grote hoop gooien, is niet productief.
Het was overtuigender geweest om de effecten van de definities in beeld te brengen aan de hand van eerdere analyses van RIVM en CBS van de effectiviteit of effecten te illustreren met enkele eigen, gestyleerde voorbeeldberekeningen en plaatjes.
Verder kon ik niet zo gauw de 8% effectiviteit in 2022 reproduceren. Zouden jullie dat nader kunnen toelichten? Het werd me bij mijn pogingen wel duidelijk dat de berekening heel gevoelig is voor de aanname van 7% onderrapportage. Dat is ook enigzins alarmerend.
We draaien de cijfers die we hebben binnenstebuiten en persen ze uit tot de laatste druppel. We zien graag jouw methode en data tegemoet zodat we zuiverder kunnen werken.
Over die 8%: dat soort lage percentages schieten al gauw alle kanten op, je moet er niet teveel waarde aan hechten.
Er komt morgen of overmorgen een nieuw artikel waarin de VE wat preciezer wordt berekend.