Het RIVM gaat ervan uit dat er in 2021 iets is gebeurd waardoor de sterftekansen in Nederland zijn verhoogd, ook voor 2024. Dat is te lezen uit de cijfers van de verhoogde sterfteverwachting (baseline), waarbij ook hogere overschrijdingen worden voorzien. De oorzaak wordt niet benoemd of toegelicht.
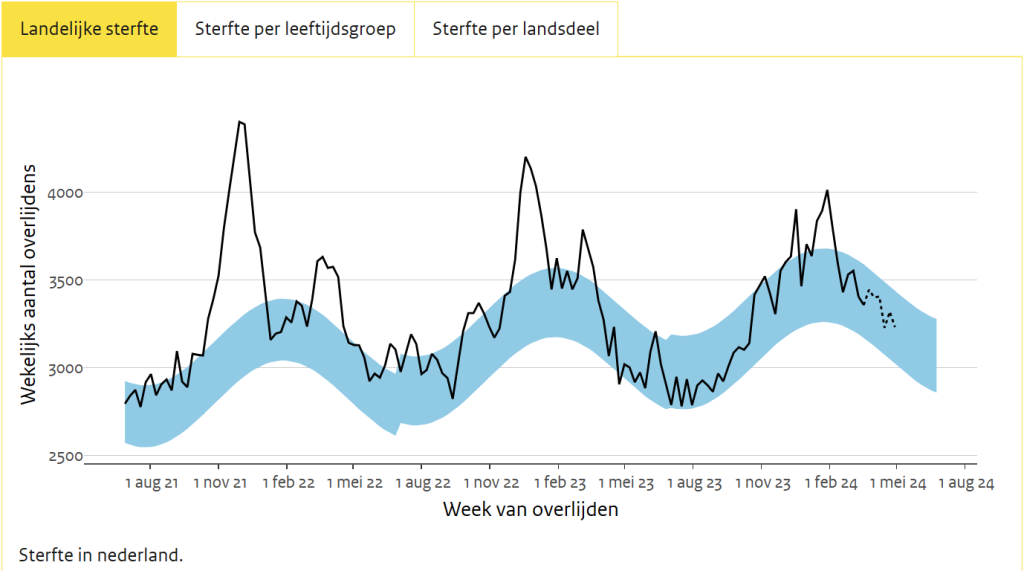
De grafiek “Landelijke sterfte” werd in de coronaperiode tijdelijk door het CBS verzorgd wegens onenigheid met het RIVM met betrekking tot doel en inhoud. Daaruit valt op te maken dat het een belangrijk communicatiemiddel is. Bij de grafiek, zoals die tegenwoordig weer door het RIVM wordt gepresenteerd, staat een (vernieuwde?) publieksuitleg. Enige aanvullende achtergrondkennis is wel vereist om goed te kunnen begrijpen wat men wil zeggen maar vooral: wat er daadwerkelijk staat. En wat er niet staat.
De tekst heb ik voor de zekerheid vereeuwigd in een screenshot. Je hoeft het niet te lezen, ik citeer de relevante stukjes in de tekst.
De baseline is verdwenen
Wat als eerste opvalt is dat in de RIVM-grafiek geen baseline meer wordt weergegeven. Het lijkt een detail maar zo’n lijn valt niet per ongeluk weg, daar wordt echt wel over nagedacht. De baseline is de verwachting van het exacte gemiddelde voor die betreffende week. Weggedesigned.
Met een baseline als referentie kun je meteen zien of de werkelijke sterfte boven of onder de verwachting voor een bepaalde week zit. Als de werkelijke sterfte een half jaar of een jaar boven de baseline blijft, dan is dat zonder hulplijn niet goed meer te zien.
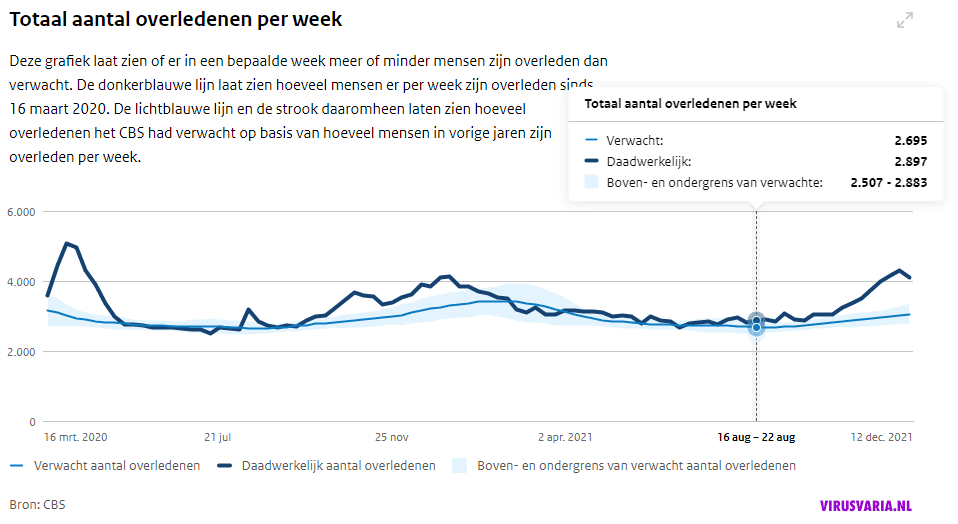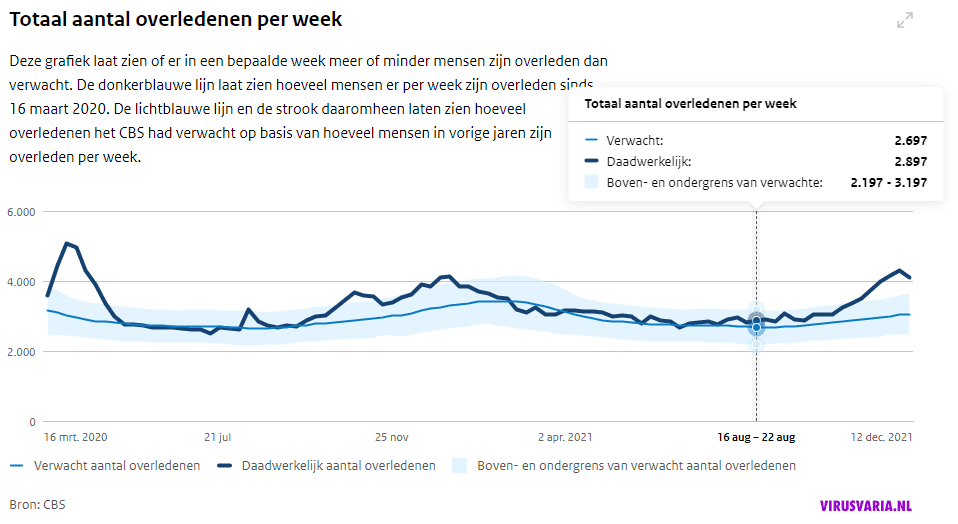
Ter herinnering een afbeelding van de RIVM-grafieken oude stijl: met baseline, de blauwe lijn middenin de bandbreedte. Ik laat nu het plaatje zien van toen men met de bandbreedte had gerommeld. Geheel per ongeluk natuurlijk, een conversiefout waardoor de oversterfte optisch werd weggewerkt. (Destijds hier gesignaleerd). Aan die bandbreedte wordt nu weer gemorreld.
Het nut van de bandbreedte: signaalwaarde
De nieuwe RIVM baseline met bandbreedte is gebaseerd op de afgelopen vijf jaar (excl. 2020), jaren waarin zich veel onbegrepen sterfte voordeed. Met die cijfers is een hoge sterfte gemodelleerd. Misschien omdat een sterftevoorspelling op basis van de afgelopen jaren er nu eenmaal bij hoort, terwijl niemand nog lijkt te weten waarvoor zo’n schatting nou eigenlijk diende. Of ze weten iets wat wij nog niet weten: de oversterfte blijft nog wel even, wen er maar aan.
De bandbreedte gaf altijd de norm aan waarbinnen de sterftecijfers van een gezonde bevolking zich zouden moeten bewegen. Elke overschrijding van die bandbreedte dient als een alarmsignaaltje. Het geeft aan dat er die week ongebruikelijk hoge sterfte plaatsvindt. Daarvoor wordt dan een oorzaak gezocht: meestal een hittegolf of een griepgolf. Een heftige griepgolf kan wel 10 weken duren. Door dat goed te monitoren hou je zicht op de volksgezondheid en kun je gepaste actie ondernemen als dat nodig is en ook weer zien wanneer het weggaat.
Komt er echter een griepgolf voorbij en de sterfte blijft desondanks netjes binnen de bandbreedte, dan heb je helemaal niets aan je voorspelling, dan was je band te breed om als signaalwaarde te gebruiken. Je toont dan alleen dat je aan je verplichtingen heb voldaan: keurig voorspeld, zelfs de griepgolf valt erbinnen.
- Je installeert geen versleten zonnepanelen op je dak als je milieubewust bezig wil zijn.
- Je hangt geen fop rookmelders op om aan de brandveiligheidseisen te voldoen.
- Je berekent geen referentie voor de volksgezondheid op basis van rampzalige jaren.
Tenzij je weet dat het foute boel is maar je wil bijvoorbeeld geen paniek veroorzaken, om maar eens een overweging te noemen. Dan ga je manieren zoeken om de normen verhogen zodat de signaalwaardes minder vaak worden aangetikt. Daar heeft het alle schijn van.
Bandbreedte is King – maar welke dan?
Het RIVM legt uit wat de bandbreedte weergeeft. Daarbij wordt de verwachte sterfte alleen genoemd als hulpmiddel om de marge te berekenen. Die verwachte sterfte is gebaseerd op de afgelopen vijf jaar – met uitzondering van 2020 want daarvan weten we dat er een coronapiek was dus dat telt niet mee, is de redenering. Maar waarom niet eigenlijk niet? De oversterftejaren 2021 en 2022 (en straks ook 2023) tellen ze wel degelijk mee en de oversterfte was in die jaren nog hoger dan in 2020, kijkend naar de seizoensjaren. Of neem als referentieperiode de afgelopen 10 jaar, dat zou het effect van die gekke laatste oversterftejaren ook wat dempen.
De statistici van CBS denken er anders over. Die nemen ook 2021 en 2022 niet mee in de prognose, omdat het duidelijk afwijkende jaren zijn. Volgens hun door Covid, maar ja, dat zijn geen medici.
Er zijn dus redenen voor het agentschap van het Ministerie van Volksgezondheid, het RIVM, om dat hogere sterfteniveau te accepteren en te ‘normaliseren’ zoals we dat ook met het winterseizoen hebben gedaan. Als ze meersterfte zouden willen maskeren, hadden ze het niet beter kunnen aanpakken.
Hieronder de RIVM-uitleg van de bandbreedte.
De band geeft de verwachte sterfte weer tussen een bovengrens en een ondergrens. De bovengrens is de verwachte sterfte plus twee standaarddeviaties ten opzichte van de verwachte sterfte. De ondergrens is de verwachte sterfte min twee standaarddeviaties ten opzichte van de verwachte sterfte.
https://www.rivm.nl/monitoring-sterftecijfers-nederland
Daar ljjkt verder geen beleid achter te zitten. Droge statistiek. Laten we dat eens narekenen aan de hand van het downloadbestand van RIVM van deze week.
Ook in dat bestand staat geen verwachte sterfte, alleen de gerealiseerde weeksterfte en de boven- en ondergrenswaarde voor elke week. De waarde die daar precies tussenin ligt is normaliter de verwachte waarde en dat is voor de laatst gerapporteerde week: 3230.
“Twee standaarddeviaties van de verwachte sterfte”. Bij een losse waarde spreken we van de ‘onzekerheid’ en die is 2 maal de wortel uit 3230 en dat is: 114.
De bovengrens zou -als het alleen om deze week zou gaan- iets moeten zijn van: 3230 + 114 = 3344. Maar de bovengrens die RIVM opgeeft is maar liefst 95 hoger: 3439, dat klopt ook met de grafiek. De signaalwaarde is dus met deze bovengrens véél minder gevoelig, van 114 naar 209.
Er moeten nu dus in één week 95 extra overlijdens meer plaatsvinden (85% meer!) om tot ‘verhoogde sterfte’ te komen, dan de onzekerheid van de weekwaarde op zich. Daar zal best een reden voor zijn, maar wat willen we nu: een signaalwaarde neerzetten om afwijkingen van de verwachting te signaleren of willen we de oversterftejaren normaliseren, door die verhoogde sterfte alvast in de verwachting mee te nemen?
Het lijkt erop dat het RIVM vooral goed wil voorspellen.
De oversterfte wordt verwacht en verdwijnt zo uit de signalering.
Nu zal de “publieksuitleg” op de RIVM-website ongetwijfeld een simplificatie zijn van de werkelijke rekenmethode waarin meer onzekerheden op een of andere manier worden meegenomen, waardoor de band wat wordt verbreed. Ook in statistiek moeten keuzes worden gemaakt, en zelfs “standaarddeviatie” is een kneedbaar begrip: welke periode neem je, welke pieken neem je wel of niet mee. En neem je een piek niet mee, top je die dan af op de bovenwaarde of zet je die op nul: de sterfte is immers ‘verklaard’ en kan worden weggeboekt uit de prognose, net als een hittegolf. Maar het valt op dat er consistent wordt toegewerkt naar een opgaande lijn.
We wisten al dat de baseline is verhoogd omdat het RIVM de jaren met onverklaarde oversterfte meeneemt in de verwachting, in tegenstelling tot hoe CBS rekent. Dat op zich is al zorgwekkend. Je mag daarbij verwachten dat de bandbreedte in absolute zin wat meegroeit, als percentage van de verhoogde aantallen. Maar dat percentage zelf stijgt toch niet van het ene jaar op het andere?
Wel dus. Ik laat het zien, weer aan de hand hetzelfde csv-bestand. Vergelijken we de eerste weken van januari, dan zien we dat de bandbreedte (2x de standaarddeviatie) groter wordt ten opzichte van de verwachte sterfte. Hetzelfde geldt voor de eerste weken van juli.
| Bovengrens als percentage van de verwachte sterfte | ||
| Jaar | 1e week januari | 1e week juli |
| 2021 | 12.9% | |
| 2022 | 11.0% | 13.7% |
| 2023 | 11.8% | 14.1% |
| 2024 | 12.1% | |
Nota bene: Ik doe het percentueel, dat is heel coulant want de standaarddeviatie wordt verhoudingsgewijs kleiner bij grotere getallen. Wortel 4 = 2, dat is 50%. Wortel 9 = 3, dat is 33,3%. Wortel 16 = 4, dat is 25%. Dat de bandbreedte daarentegen percentueel juist toeneemt bij hogere getallen behoeft dus wel wat uitleg.
Zelf berekenen?
Het enige wat erbij komt kijken in optellen, aftrekken, delen en vermenigvuldigen. Dat is leuk! 🙂
- Bereken eerst in een kolommetje de baseline (bovengrens+ondergrens gedeeld door 2).
- In de kolom daarnaast doe je bovengrens minus baseline. Dat geeft dan weer hoeveel overlijdens er nog binnen de bandbreedte van 1 week vallen.
- Als je dat in een volgende kolom weer deelt op de baseline heb je het percentage (zie je wel dat het niet zo moeilijk is)
De bovengrens was in de 1e week van januari 2022 11% hoger dan de verwachting in die week. In 2024 is de bovengrens 12.1% geworden. Van 11 naar 12,1, dat is een verhoging van 10% in twee jaar tijd, bovenop de toch al verhoogde baseline. Er kunnen, alleen al door deze ogenschijnlijk minimale verbreding van de band, elke week 40 mensen meer doodgaan zonder dat er ‘verhoogde sterfte’ wordt gesignaleerd.
In één jaar tijd zijn dat ook weer ongeveer 2.000 overlijdens extra. Terwijl de verhoging van de baseline al ca. 9.000 extra overlijdens toestond in 1 jaar, gerekend van juli 2023 t/m juni 2024. (Om dat te berekenen heb je ook traditionele “virusvaria-baseline” nodig die we op sterftemonitor.nl gebruiken, zie ook ResearchGate).
Het totaal aan extra ‘ongemerkte oversterfte’ komt dan op jaarbasis op ca. 11.000 overlijdens meer dan voorheen. Dat zijn getallen waarbij een griepepidemie verbleekt en het zit in de orde van grootte van coronajaar 2020, met twee coronagolven in 1 kalenderjaar. In de toekomst zal er heel wat oversterfte aan de aandacht van de media ontglippen.
Dus:
- De verwachting is verhoogd
- Bij een hogere verwachting zou de bandbreedte nog niet eens percentueel mee moeten groeien
- De bandbreedte wordt echter een steeds grote percentage van de verwachting. De signaalwaarde wordt verder verhoogd waardoor nóg meer oversterfte onopgemerkt blijft.
Zou de bandbreedte misschien verhoogd zijn omdat er zoveel pieken waren, en zoveel aanhoudende oversterfte? Pieken worden niet meegenomen zegt het RIVM. Als ze daarmee alleen het gedeelte boven de bovenmarge bedoelen, blijft er nog veel oversterfte over tussen baseline en bovenmarge. En als het op basis van reële cijfers is, zou de ondermarge dan niet veel kleiner moeten worden omdat er vrijwel geen ondersterfteweken waren in de afgelopen vijf jaar? Of wordt dat dan wél weer hard statistisch doorgemodelleerd? Zoals de ondermarge nu wordt gepresenteerd is de enige functie: het spiegelen van de bovenmarge. Dat terzijde.
Hoe belangrijk is die bandbreedte nou?
De baseline wordt niet meer gehanteerd, alles wordt opgehangen aan de bandbreedte. De lichtblauwe bandbreedte is het veilige gebied, overschrijding daarvan geeft “licht verhoogd” aan. In voetnoot 3 legt het RIVM uit hoe we dat gradueel moeten zien:
“Als de sterfte hoger is dan 2 standaarddeviaties boven de verwachte sterfte, noemen we de sterfte licht verhoogd. Bij 3 standaarddeviaties noemen we de sterfte verhoogd. Bij 4 of meer standaarddeviaties noemen we de sterfte sterk verhoogd.”
https://www.rivm.nl/monitoring-sterftecijfers-nederland
Wat er niet bij staat is dat deze signaalwaarde alleen geldt op weekniveau. Voor wetenschapscolumnisten en spin-dokters van het CBS is dat een dankbaar anker dat 52 keer per jaar kan worden uitgegooid, maar voor mensen die een beetje kunnen rekenen ligt dat anders. Neem je langere periodes, dan wordt de bandbreedte namelijk kleiner (denk ook aan de Wortel-berekening). Toch kijken RIVM en CBS week na week opnieuw uitsluitend naar alleen de laatste week. Vergelijk het met een muntje opgooien. Vrij naar een eerdere post Bandbreedtes voor dummies:
Gooi je 28 keer het muntje op en je krijgt bijvoorbeeld 24 keer kop of 24 keer munt, dan is dat een signaal dat er iets met je munt aan de hand is (die kans is 0.0153%, je zou ca. 700.000 moeten gooien om zo’n reeks tegen te komen). Dan zul je ofwel je verwachting wat deze munt betreft moeten bijstellen ofwel de munt afkeuren en gaan onderzoeken. Als je dan toch stug volhoudt ”ja maar elke keer dat ik gooide was het toch echt een kans van een op twee dus er is niets bijzonders te zien” dan pas je de verkeerde regel toe en sluit je je ogen voor de reeks die je aan het maken bent.
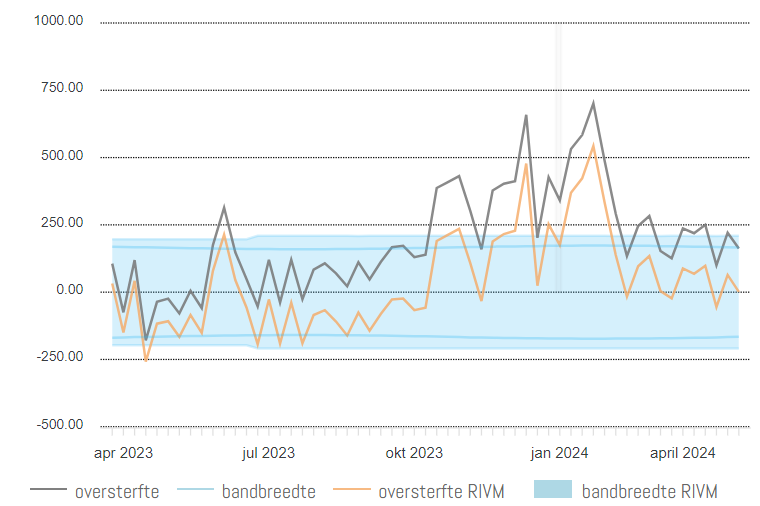
RIVM en CBS beschouwen elke week als op zichzelf staand, terwijl er bijvoorbeeld sinds oktober 2023 tot nu (32 weken) slechts in 4 weken een sterftecijfer was dat lager was dan de (verhoogde) verwachting, en in 28 weken hoger. Dat is de oranje lijn. Kijken we naar de oversterfte op basis van de traditionele verwachting (grijze lijn in de grafiek), zoals die vóór 2024 werd berekend, dan is de sterfte sinds juli 2023 niet één keer onder de baseline gekomen. Een onafgebroken meersterftereeks van ca. 40 weken: significante oversterfte.
Wat het RIVM precies onder een “standaarddeviatie” verstaat, weten we dus niet precies genoeg om na te kunnen rekenen. Het is voor hen in elk geval iets wat groeit naarmate er meer mensen doodgaan, net als de onzichtbaar gemaakte baseline. Het is een mix tussen harde statistiek (de ondermarge die even groot is als de bovenmarge) terwijl er anderzijds naar de realiteit wordt toegerekend vanwege de verhoogde overschrijdingen aan de bovenkant. En dan gaat de onderkant weer mee natuurlijk want dat hoort zo met statistische onzekerheidsmarges…
Waar staan we nu?
Zie de oranje lijn voor 2024. De X-as van deze grafiek (dank aan Herman Steigstra) gaat van augustus t/m juli. Seizoensjaren geven een duidelijker beeld omdat de winterbobbels niet worden doorsneden door de jaarwisselingen. In ’22-’23 (groene lijn) was er iets minder oversterfte dan in ’21-’22 en nu zitten we weer iets lager. Maar nog steeds ver boven coronaseizoen ’19-’20. En ook boven ’20-’21, toen iedereen werd gevaccineerd.
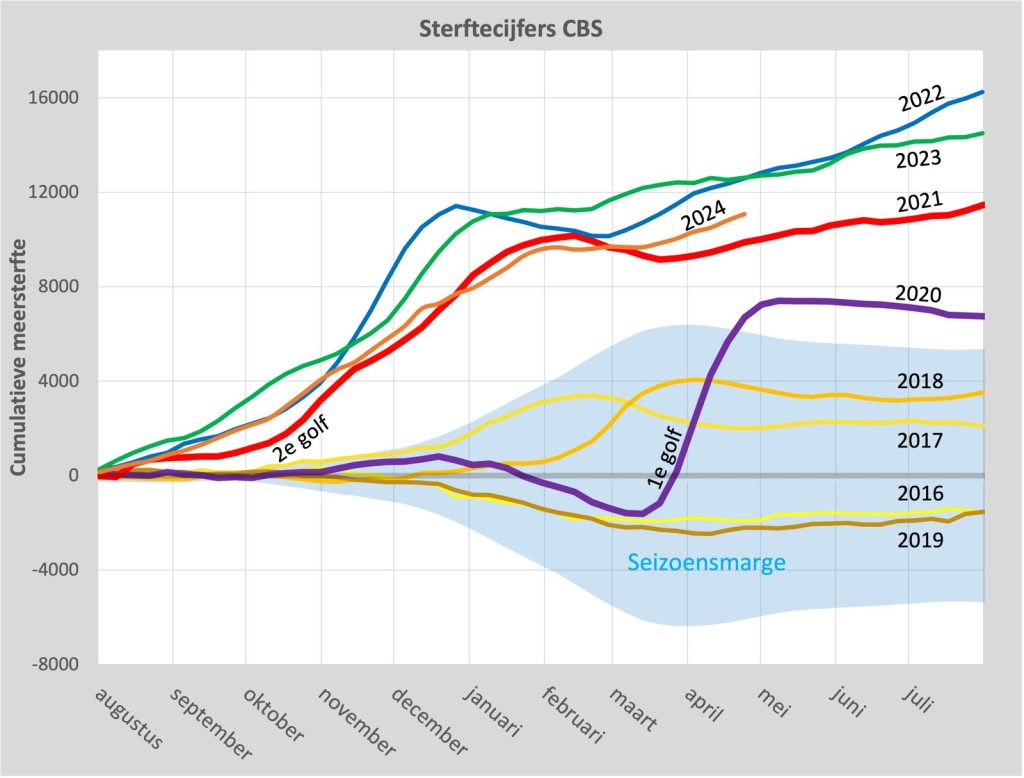
Wat ik vooral akelig vind aan deze grafiek: Vóór 2021, bijvoorbeeld in de zomer na de 1e golf, daalt de lijn weer (ondersterfte) na de oversterfteperiode. Dat zie je ook na de bulten in 2017 en 2018: een kleine daling en dan stabilisatie.
Maar daarna, in 2021, 2022 en 2023 stijgt het gewoon door in de zomer. Dat zit echt niet goed. Dat daar geen aandacht aan wordt besteed betekent voor mij dat ze er niets meer aan kunnen doen. Het is geaccepteerd, een fait accompli. En het gaat wéér gebeuren. Als dat iets te maken heeft met het beleid, dan zit er niets anders op dan volhouden dat ze juist hebben gehandeld en zwangeren gewoon weer adviseren om de prik te nemen. Er ontstaat anders een cognitieve dissonantie die niet te managen is.
Verder vooruit gekeken
Mocht de sterfte in de komende jaren toch weer langzaam terugzakken naar het normale peil, dan zal het RIVM ondersterfte gaan rapporteren totdat dat al te gortig wordt en ze de baseline weer terugcorrigeren omdat het zo goed gaat. Er is dan in elk geval een hoop oversterfteheisa gemist. Laten we duimen dat we daarop geen jaren hoeven te wachten en dat we dan ook weer een beetje in lijn komen met niveau pre-2020. Deze grafiek biedt vooralsnog weinig hoop op zo’n verbetering.
In het vorige artikel zagen we dat de gemiddelde overlijdensleeftijd in 2021 en 2022 vijf jaar lager lag dan voorheen.
Als we sommige doemscenario’s moeten geloven (Vandenbossche, Dowd, Cole, McCullough, McKernan, Bonte etc.) kan het sterfteniveau nog decennialang hoger blijven. Dat zal moeten blijken. Met het verhogen van de baseline heeft het RIVM daar dan in elk geval wel al veilig op voorgesorteerd. Dat doen ze niet voor niets: ze weten het eigenlijk al, dat is uit de cijfers af te lezen.
Vragen over de gebruikte technieken om minder oversterfte te signaleren:
- Waarom gebruikt het RIVM andere vergelijkingsjaren jaren dan het CBS, waardoor er een hogere sterfteverwachting (baseline) wordt verkregen?
- Wat is de onderbouwing van de verruimde onzekerheidsmarge, waardoor de signaalwaarde voor oversterfte verder van de baseline komt te liggen?
- Deze marge wordt jaarlijks een tikje verder opgerekt, meer dan wat op basis van de baseline verwacht kan worden. Vanwaar deze sprongsgewijs toenemende tolerantie, steeds in juli?
- Weken werden door het CBS niet als reeks maar als losstaande gebeurtenissen beoordeeld waardoor langdurige oversterfte niet werd gesignaleerd. In de gezondheidssector is het meewegen van de historie noodzakelijk voor een diagnose. Blijft het RIVM uitsluitend naar overschrijdingen van de weekmarge kijken?
- Het RIVM toont geen baseline in de grafiek, wat het visueel signaleren van meersterfte en oversterfte (met name over meerdere weken) bemoeilijkt. Kan het RIVM die lijn weer terugbrengen en zo niet, wat is daarvoor de overweging?
Waar de jarenlange oversterftegolf vandaan is gekomen, tienduizenden overleden mensen, daar zal het Rijksinstituut voor Volksgezondheid en Milieu, als agentschap van het Ministerie voor VWS, geen uitspraak over doen. De verwachting klopte, zal dan de constatering zijn.
Als dat geen eredoctoraat of wetenschappelijke penning van uitzonderlijke verdienste waard is, weet ik het ook niet meer.




Zou het RIVM er een schaduwboekhouding op na houden? Want zo gaan ze natuurlijk griep- en hittegolven missen (dan wel alleen de pieken ervan signaleren).
Tot dec. 2023 stelde het RIVM dit op de pagina https://www.rivm.nl/monitoring-sterftecijfers-nederland :
“Sinds de griepepidemie van 2009 houdt het RIVM wekelijks het aantal overleden mensen in de gaten met gegevens van het CBS. Het doel van het monitoren van sterftecijfers is om de impact van een epidemie of een incident in beeld brengen. In het verleden zijn er pieken in de totale sterfte te zien bij koude- en hittegolven en bij uitbraken van infectieziekten, zoals griep.
De oversterfteschattingen van het CBS en het RIVM kunnen op weekniveau verschillen.
⦁ Het CBS kijkt naar de gemiddelden over de afgelopen jaren voor de betreffende week, deze zijn inclusief verhoogde sterfte in het griepseizoen.
⦁ Het RIVM wil juist ook elk jaar oversterfte door de griep in kaart brengen. Om die reden verschillen de schattingen van het CBS en van het RIVM. ”
Nu stelt zij:
“Het RIVM en het CBS houden sinds 2009 elke week het aantal overleden mensen in Nederland bij. Hiermee kunnen de gevolgen van bijzondere omstandigheden op het aantal overleden mensen in beeld gebracht worden. Bijvoorbeeld bij een hitte- of koudegolf, een griepgolf of de uitbraak van een infectieziekte. “
En heel veel dank, Anton, voor de signalering en de uitleg. Het is zeer wrang dat dit in de “gewone media” niet eens opgemerkt werd en wordt.
inmiddels meer onderzoek: oversterfte moet onderzocht want lijkt te komen door de prikken:
“Conclusions Excess mortality has remained high in the Western World for three consecutive years, despite the implementation of containment measures and COVID-19 vaccines. This raises serious concerns. Government leaders and policymakers need to thoroughly investigate underlying causes of persistent excess mortality.”
https://bmjpublichealth.bmj.com/content/2/1/e000282
Ja er komen er steeds meer. Ik zal binnenkort een aantal verzamelen en in een artikel op een rijtje zetten.
Ik zie dit nu pas, heel interessant, dank je wel! Maar ik ben verwonderd over de bewering dat “de ‘onzekerheid’ […] is 2 maal de wortel uit 3230”. Zoiets heb ik nog nergens eerder gezien.
Gewoonlijk is de standaard onzekerheid (SD) gebaseerd op de afwijkingen (deviaties) van het gemiddelde – en niet de wortel van het gemiddelde. Als de data in Excel of Openoffice gestopt wordt dan kan daarmee de standaarddeviatie eenvoudig berekend worden. Wel is het gebruik door RIVM vager, omdat ze griepgolven niet meenemen (of meenamen?). Zo vindt ik bijvoorbeeld in de door jou gebruikte .CSV voor mei t/m september 2023 met =STDEV(B98:B119) een grieploze sample standaarddeviatie van 103.6, dus twee SD is 207. Het RIVM neemt, als ik het goed begrijp, (D141-C141)= 419 als bandbreedte voor 2024, dat is twee maal twee SD zodat 2*SD=209.5 en daar lijkt me niks mis mee.
In tijden met meer fluctuatie is de standaardeviatie groter dan voorheen, per definitie. Maar of dat nu “normaal” gevonden moet worden, dat is natuurlijk evengoed een punt waar over te twisten valt. Ik vind van niet, met dezelfde argumenten als waarom de nu “gewoon” geworden oversterfte niet “normaal” gevonden moet worden.
‘of dat nu “normaal” gevonden moet worden, dat is natuurlijk evengoed een punt waar over te twisten valt.’ Dat is inderdaad het belangrijkste punt. Zie ook de verbredingen van de marges.
De inmiddels t/m wk 43 (eind oktober) zichtbare verwachting van RIVM vertoont vanaf wk 35 een opvallend steilere curve dan voorgaande jaren. Daar blijven de te verwachten “herfsthobbels” dan mooi tussen, maar blijven de piekjes van hittegolven toch nog zichtbaar.