In den folgenden Diagrammen werden die Bevölkerungsdaten von NIMS verwendet. Infolgedessen können die Sterblichkeitsraten unter den Ungeimpften, zumindest in einigen Altersgruppen, niedriger sein, als sie tatsächlich sind.
Da England mit unreinen Bevölkerungsschätzungen arbeitet, wissen wir nicht, wie viele ungeimpfte Menschen es gibt. Die verwendete Bevölkerungsgröße wirkt sich direkt auf die Berichterstattung über ungeimpfte Personen aus. Die Abweichung unterscheidet sich auch je nach Altersgruppe. Es ist noch nicht klar, ob und wenn ja, wie dies angepasst werden kann; daran arbeitet die UKSHA (UK Health Security Agency). Das ONS sagt:
"Wir hoffen, dass die Arbeit der UKHSA zur Verbesserung der NIMS-Daten (einschließlich der Entfernung von Duplikaten) zusammen mit der Arbeit des ONS an Bevölkerungsschätzungen und der Volkszählung 2021 unser Verständnis verbessern wird. Es ist wirklich positiv, dass ONS und UKHSA zusammenarbeiten, um eine Lösung für dieses Problem zu finden, das für so viele Statistiken so wichtig ist. Angesichts dieser Unsicherheit kann das Wissen um die Auswirkungen der verschiedenen Optionen den Nutzern helfen, die präsentierten Daten mit Vorsicht zu interpretieren."
Eine ausführlichere Begründung finden Sie im Beitrag "Britischer Professor: "Daten zur Sterblichkeit nach Vaxx-Status sind Schrott" „
Hoffen wir, dass die Deduplizierung durchgeführt wird, ohne die Auswirkungen auf die Impfeffekte mit einem halben Auge zu betrachten. Es wäre klug, einen unabhängigen Betreuer zu organisieren (Prof. Fenton möchte wahrscheinlich helfen), sonst wäre es eine ebenso machtlose Operation wie die Übersterblichkeitsstudie von CBS/rivm.
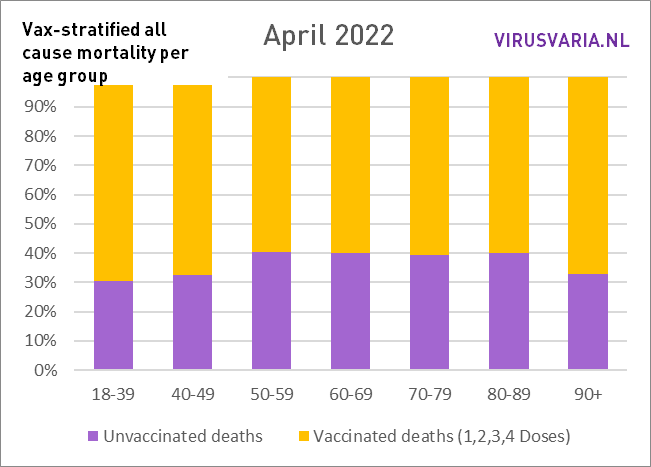
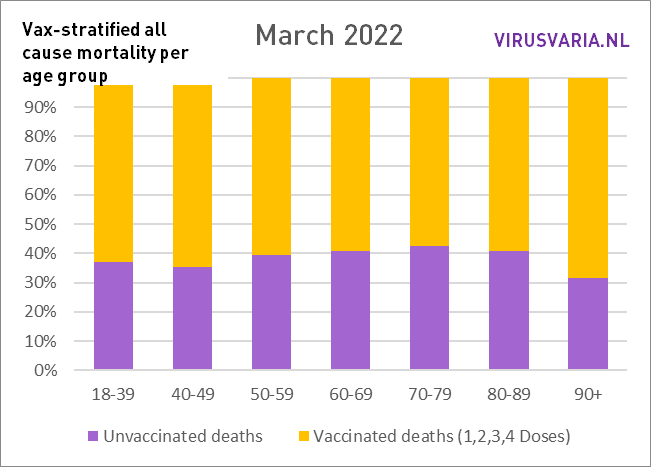
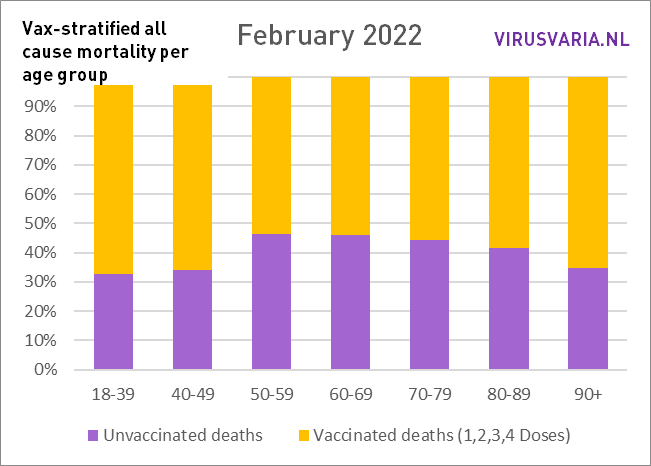
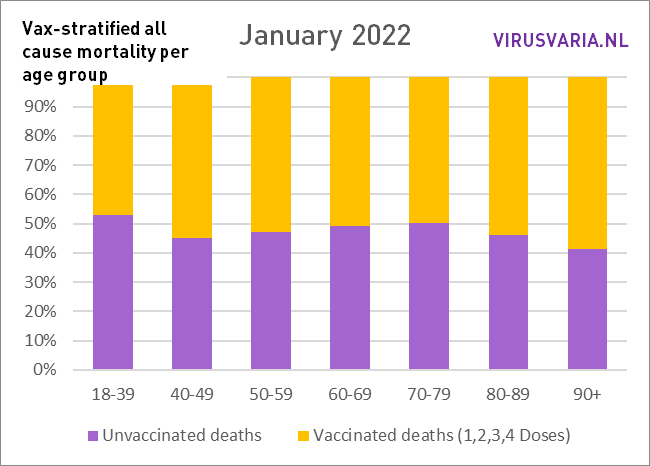
Wie läuft es in den Ländern, die wichtige Persönlichkeiten öffentlich machen? Die britischen Daten sind aussagekräftig, wenn man sie grafisch darstellt. Sie sprechen für sich selbst, scrollen Sie gerne durch. Es wurden keine weiteren Korrekturmethoden angewendet. Dies war nicht erforderlich, da keine Altersgruppen aufsummiert wurden und daher beispielsweise auf Personenjahre zurückgegriffen werden muss. Solche Änderungen sind erforderlich, wenn Verallgemeinerungen zur „Sterblichkeit“ vorgenommen werden müssen. Da wir es nun mit einer Krankheit zu tun haben, die besonders altersdiskriminierend wirkt, macht das wenig Sinn. Es ist wichtig, die einzelnen Altersgruppen im Auge zu behalten.
Es gibt ein methodisches Problem: Die Mortalität wird in 10-Jahres-Kohorten angegeben. Insbesondere im Alter zwischen 70 und 90 Jahren wird dies dazu führen, dass Aussagen über beispielsweise 70-79 Jahre getroffen werden können, während in der ältesten Gruppe 75-79 die Sterblichkeit möglicherweise dreimal so hoch ist wie in der jüngsten Gruppe 70-74. Dafür ist die Berichterstattung zu grobgranular. Das ist schade – aber besser als nichts.
Inwieweit unterscheiden sich diese 5-Jahres-„Unterkohorten“ tatsächlich voneinander? In Bezug auf die Vax-Prozentsätze gibt es ohnehin nur einen geringen Unterschied (ca. 2 %) zwischen den jüngsten „Unterkohorten“ und den ältesten über 50-Jährigen.
Bei hochbetagten Menschen liegt die Vax-Rate bei bis zu 95 %. Es kann nicht behauptet werden, dass die 5 %, die die Injektion nicht erhielten, bereits viel gesünder waren und daher eine geringere Sterblichkeit verursachten. Im Gegenteil: Fast jeder in den höheren Altersgruppen ohne Kontraindikation hat sich eine Spritze gespritzt.
Bei den jüngeren Altersgruppen könnte das anders sein, dort ist der Unterschied in der Sterblichkeit aber deutlich geringer (z. B. zwischen 40-44 und 45-49), so dass dort kaum ein Problem auftritt. Es ist zwar vorhanden, erklärt aber nicht die aufgezeigten Unterschiede. Weitere Informationen zur angewandten Methode und zum vollständigen „Verwirren“. ganz unten dieser Artikel.
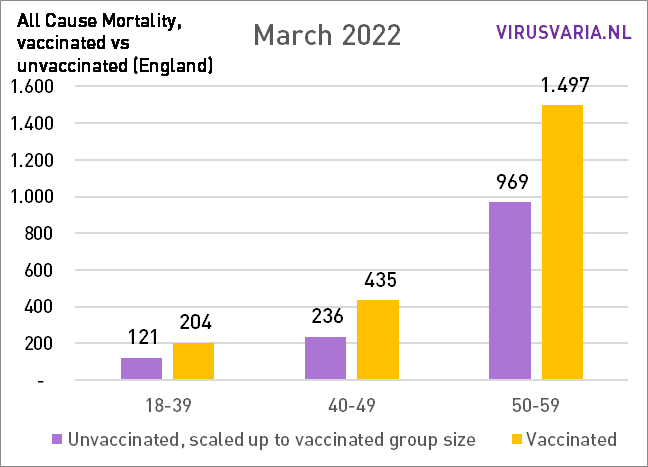
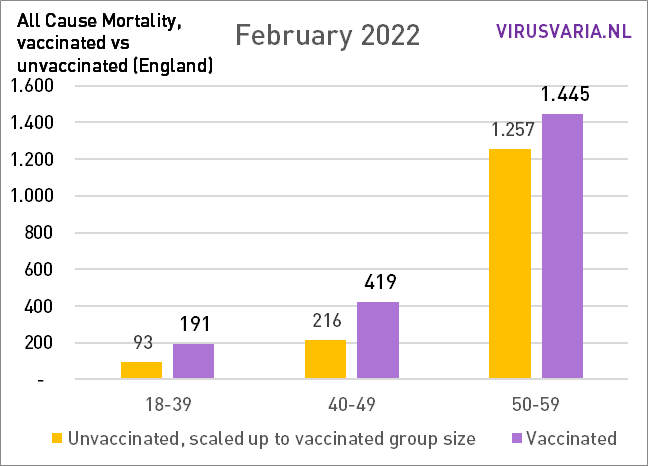
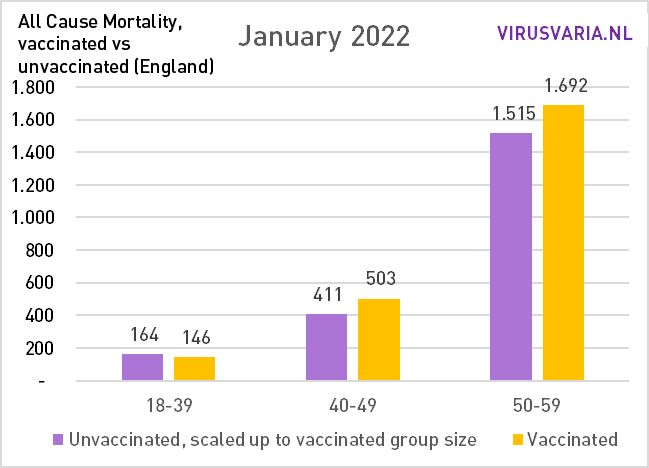
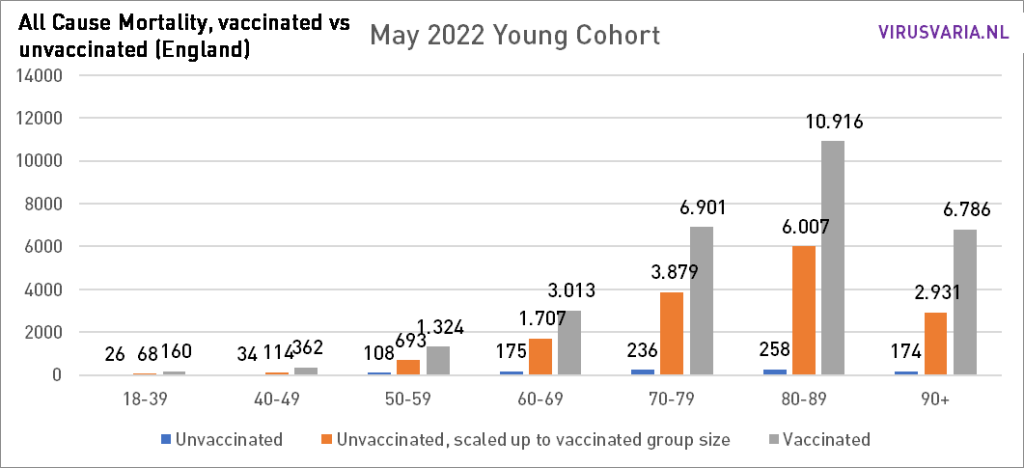
Die Grafiken lassen sich wie folgt lesen: Der violette Balken zeigt, wie viele Ungeimpfte gestorben wären, wenn die Gruppen der Geimpften und Ungeimpften gleich groß gewesen wären. Bei All Cause Mortality wird nicht zwischen Todesursachen unterschieden, es handelt sich also sowohl um Covid- als auch um Nicht-Covid-Todesfälle.
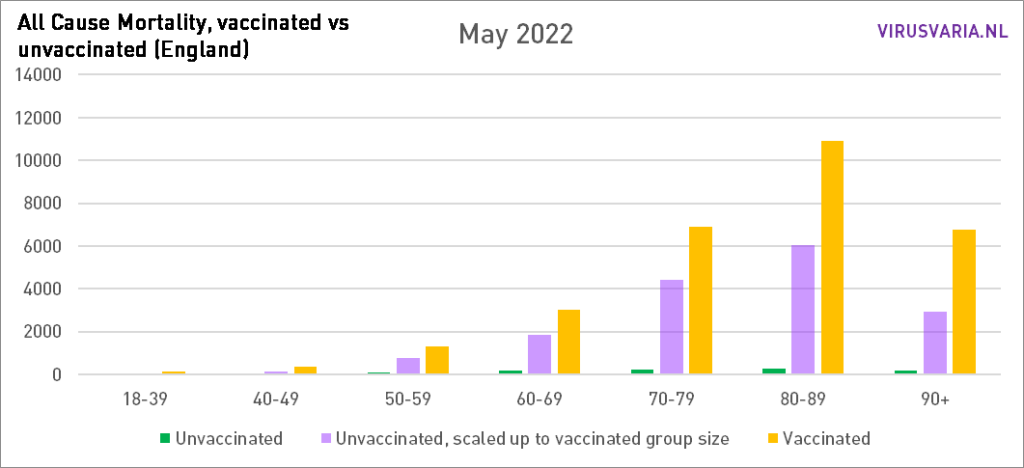
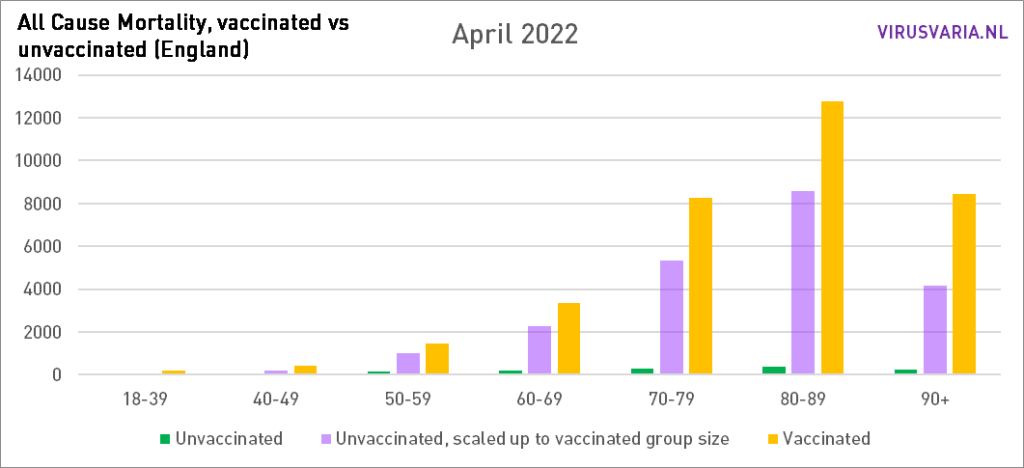
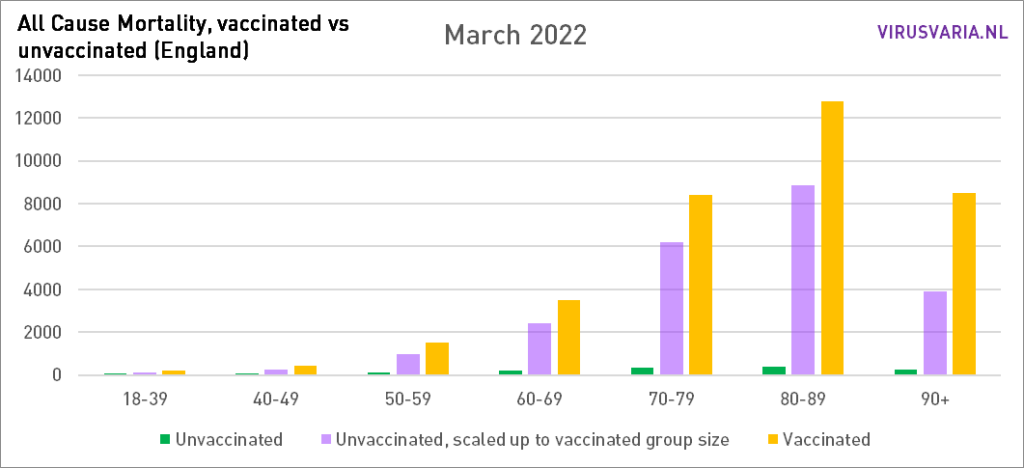
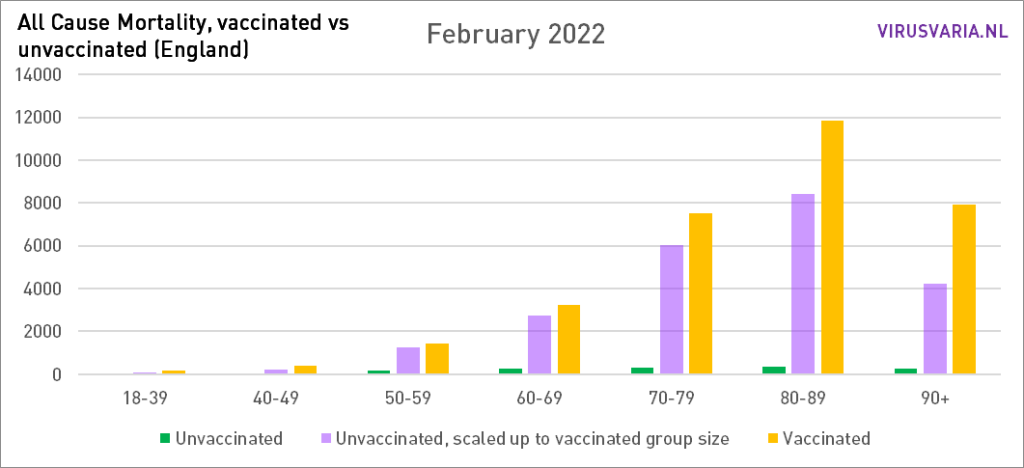
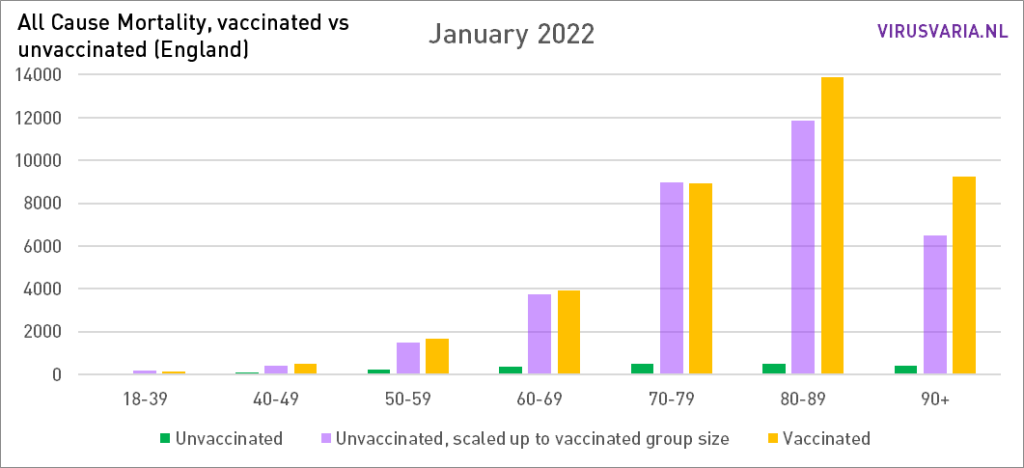
Grafiken 2021 steht hier.
Methode
Quelldaten der britischen Regierung:
1) Sterblichkeitszahlen nach Impfstatus von gov.uk: Download die Excel-Datei hier
2) Impfstatus (%) von gov.uk: Download Die XML-Version finden Sie hier (Schaltfläche unter dem unteren Diagramm)
Quelle 1 zeigt, wie viele Todesfälle in Gruppen von 10 Jahren gezählt wurden (mit Ausnahme der Gruppe 18-39). Diese werden aufgeschlüsselt in Ungeimpfte, innerhalb von 21 Tagen nach der ersten Dosis, nach 21 Tagen nach der ersten Dosis, innerhalb von 21 Tagen nach der zweiten Dosis, nach 21 Tagen nach der zweiten Dosis, innerhalb von 21 Tagen nach der dritten Dosis, nach 21 Tagen nach der dritten Dosis. Wenn man diese Untergruppen miteinander vergleichen möchte, wird es sehr kompliziert, weil zwischen der ersten Dosis und der zweiten Dosis viel mehr Zeit liegt als zwischen der zweiten und der dritten – und allein deshalb werden mehr Menschen sterben. Um nur einige zu nennen. Deshalb habe ich alle Todesfälle zusammengezählt, damit ich die Gesamtzahl der verstorbenen Geimpften kenne. Folgestudien können dann ins Detail gehen – sofern das bei einem Massaker wie diesem interessant ist.
Die oben genannten Zahlen werden erst aussagekräftig, wenn wir wissen, wie groß jede Untergruppe ist und wie hoch der Impfanteil dieser Gruppe ist. Dies ist in Quelle 2 genau angegeben. Leider ist die Einteilung sehr unterschiedlich, in 5-Jahres-Kohorten. Daraus lassen sich leicht 10-Jahres-Kohorten erstellen. Wir verlieren etwas an Auflösung, aber um es umgekehrt zu machen, bedarf es einer Art Tricks, die es weniger transparent machen und ab einem bestimmten Punkt weiß man nicht mehr genau, was man eigentlich sieht.
Darüber hinaus werden die Prozentsätze pro Tag und die Sterblichkeit pro Monat angezeigt. Als zuverlässigste Methode erwies es sich, den 15. eines jeden Monats als Referenz zu nehmen. Dies war besonders während der Kampagnen wichtig. Die Impfquoten sind mittlerweile praktisch stabil.
Dann haben wir den Impfstatus einer Altersgruppe, von der wir wissen, wie groß er ist, zum Beispiel 80 %. Das bedeutet 20 % ungeimpft. Multiplizieren Sie also Ihre Zahlen aus dieser Gruppe mit 4, um sie rechnerisch neben die Zahlen der Geimpften zu stellen. Eine andere Methode besteht darin, alles in „pro 100.000“ umzuwandeln, aber dann gehen die Verhältnisse manchmal wieder verloren.
Das ist also geschehen: In jeder Altersgruppe wurde die Zahl der ungeimpften Todesfälle (grün) und die Zahl der geimpften Todesfälle (gelb) untersucht. Basierend auf der Impfquote wurden beide Gruppen gleich groß gemacht und die Anzahl der Todesfälle entsprechend skaliert. Diese virtuelle Zahl wird durch den violetten Balken dargestellt.
Verwechselnd
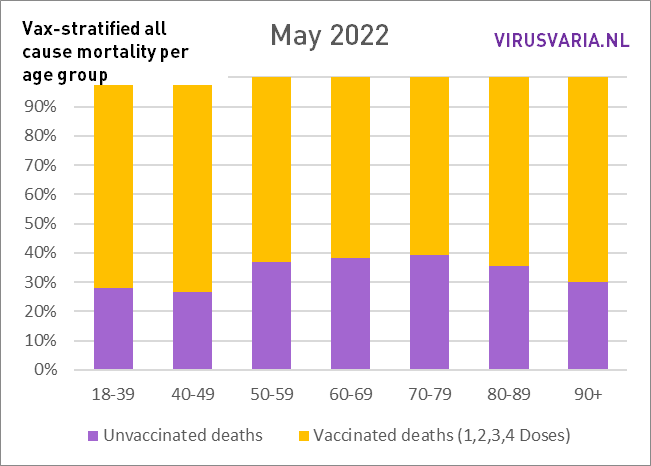
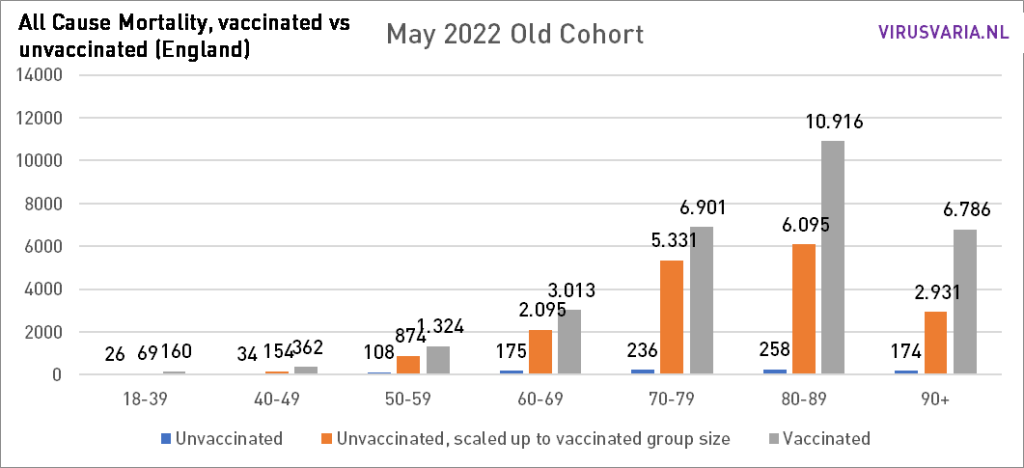
Auch innerhalb von 10-Jahres-Kohorten kommt es zu Verwirrungen. Beispielsweise könnte es sein, dass viel mehr Menschen im Alter zwischen 75 und 79 Jahren geimpft wurden als diejenigen im Alter zwischen 70 und 74 Jahren. Wenn in dieser älteren Gruppe mehr Menschen sterben, scheint es, als ob sie an den Impfungen sterben. Leider fehlen Mortalitätsdaten pro 5-Jahres-Kohorte. Allerdings gibt es die Impfquoten. Ab dem 70. Lebensjahr beträgt der Unterschied innerhalb einer Kohorte maximal 1,5 %. Der größte Unterschied besteht in der Kohorte der 40- bis 49-Jährigen: fast 5 %. (40_44: 77,02 % und 45_49: 81,87 % geimpft).
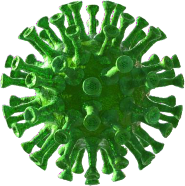
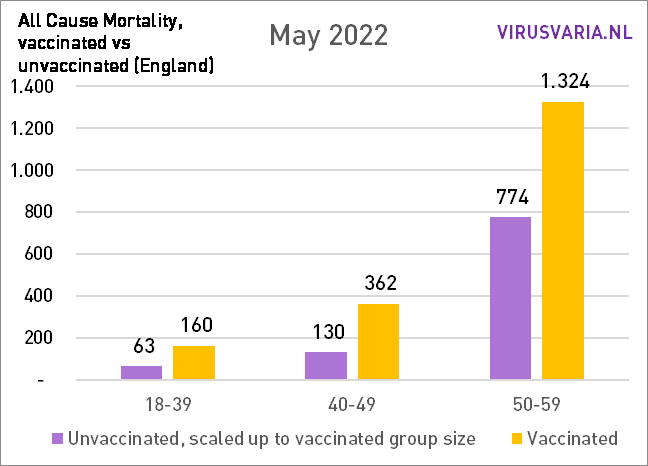
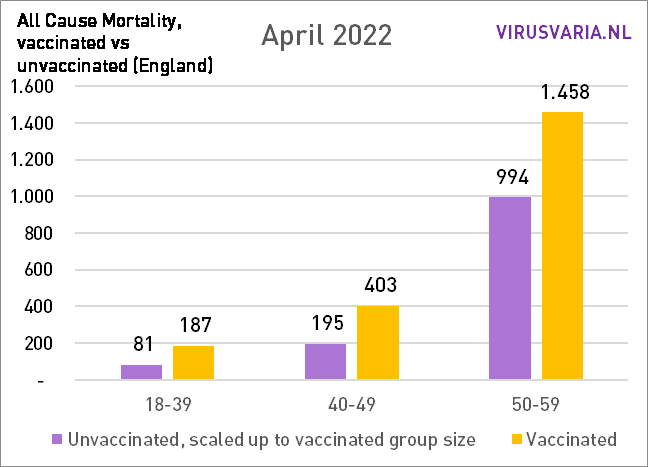
Um zu sehen, wie enorm sich die Impfquote unterscheiden würde, habe ich den gesamten Monat Mai mit der Impfrate der „jüngeren Kohorte“ und der „älteren Kohorte“ „durchgespielt“. Der größte Unterschied ist bei 70-79 zu erkennen.
Wenn die Unterschiede durch Confounder beeinflusst werden, hoffe ich, dass mir jemand erklären kann, wie sich die Unterschiede trendmäßig ändern können. Um den Trend zu sehen, können Sie sich alle Grafiken ab Anfang 2021 ansehen hier ansehen.
Ungeachtet dessen bleibt es beunruhigend.

Danke, Anton, für eine weitere gute Erklärung. Frage: Gehören Personen, die gerade zum ersten Mal geimpft wurden (<3 Wochen?), zur ungeimpften Bevölkerung?
Hallo Nanda,
Sie werden im Bericht als „innerhalb von 21 Tagen nach der Impfung gestorben“ aufgeführt. Ich habe sie daher als „geimpft“ behandelt. Sie sind dort einfach registriert. Ich verstehe Leute nicht, die es anders interpretieren. Auch wenn es um Covid/Nicht-Covid geht, sollte man diese Menschen nicht als ungeimpft betrachten.
Ich verstehe, dass sie auch separat auswertbar sein müssen.
Wenn Krankenhäuser nur mit dem Status „geimpft: ja/nein“ arbeiten, entsteht ein Problem. Aber: Mit etwas gutem Willen können Sie im GGD-Impfregistrierungssystem für jeden Verstorbenen das Datum der Impfung nachschlagen. Wenn es kein Testament gibt und man sich auf Krankenhausinformationen verlassen muss, wird es Chaos geben.
Die Bedeutung dieser ersten drei Wochen: Bei künstlicher Immunität benötigt der Körper offenbar drei Wochen, um einen Schutz aufzubauen, der vier Monate anhält. Bei einer natürlichen Infektion hat fast jeder die Krankheit nach drei Wochen überwunden und man hat eine robuste Immunität, die mindestens genauso gut funktioniert und viel länger anhält, im Prinzip lebenslang, sofern das Virus nicht mutiert und solange das Immunsystem selbst noch gut funktioniert.
Es könnte sich auch um eine Strategie handeln, wie sie bei HIV-Behandlungen angewendet wird. Wenn jemand trotz der damaligen Behandlung mit experimentellen Medikamenten schnell starb, war er offenbar bereits zu geschwächt und konnte nicht mehr gerettet werden. So wurden viele Unfälle verschleiert, heißt es zumindest in „The Real Anthony Fauci“ von Robert Kennedy Jr. Ich habe das inzwischen als wahr akzeptiert, auch weil das Buch geschwiegen wird.
Vielen Dank für diese schnelle und umfassende Antwort. Sie haben Recht, dass Sie sie als geimpft gezählt haben. Ich fand es immer seltsam, dass dies bei offiziellen Zahlen nicht der Fall war. Meiner Meinung nach zählt man dann die Menschen, die kurz nach der Injektion gestorben sind. Tod durch diese Injektion in der falschen Gruppe.
Gute Arbeit, Anton!
Interessant ist, wie lange die Übersterblichkeit geimpfter Menschen in diesen Grafiken noch zu sehen sein wird. Wird der Unterschied im Jahr 2022, 2023 kleiner? Oder wird es noch viele Jahre so groß bleiben?
Im Jahr 2021 starben vor allem in den ersten Monaten viel mehr ungeimpfte Menschen (Februar, März, April), sodass man kurzfristig davon ausgehen kann, dass der Impfstoff seine Aufgabe erfüllt hat. Danach, sagen wir, bis Oktober 2021 ungefähr gleich viel, und danach sind mehr Geimpfte gestorben.
Mal sehen!
Genau! Diese ersten Monate waren der Grund, weiter hart zu arbeiten (das können Sie auch in dem früheren Beitrag sehen, den ich jetzt aktualisiert habe). Trotz mutierendem Virus und Anzeichen von Nebenwirkungen.
Der Vax/Unvax-Unterschied ist seit Jahresbeginn gestiegen. In den folgenden Grafiken habe ich alle Altersgruppen addiert: die Gesamtsterblichkeit.
Im Mai verringerte sich die Differenz zum Vormonat erstmals leicht, allerdings nur in absoluten Zahlen!
Auch die Gesamtsterblichkeit war im Mai niedriger (ich glaube, sie schwankt erheblich...) Dadurch ist prozentual kein Rückgang zu verzeichnen, sondern es ist immer noch eine steigende Tendenz zu erkennen.
Vielleicht lohnt es sich, ihm einen Artikel zu widmen. Oder zwei: eine mit den guten Nachrichten und eine mit den schlechten Nachrichten 😉
Ich weiß nicht, ob Sie noch Benachrichtigungen über eine von mir bearbeitete Antwort erhalten. Daher diese neue Antwort. Ich werde es wieder wegwerfen. Grüße, Anton
Hallo Anton,
Ja, ich bekomme die Antworten! Nur sind wir jetzt auf Reisen, also bin ich etwas weniger auf dem Laufenden ...
Vielen Dank für diesen Zusatz. Ich bin kein Arzt, es kann sicherlich Faktoren geben, die diesen Unterschied teilweise erklären können, aber ich verstehe nicht, warum dieser Impfstoff für Omicron verwendet wird, das eine andere Krankheit zu sein scheint als die vorherigen Varianten. Sowohl im Hinblick auf den Verlauf als auch auf die Wirksamkeit der Impfstoffe.
Grüße Martin
Hallo Anton, es scheint mir eine vernünftige Annahme zu sein, dass Impfungen nicht viel (mehr?) dazu beitragen, die Sterblichkeit zu senken. Trotz der möglichen Unterschiede beispielsweise im Alter und im ursprünglichen Gesundheitszustand zwischen den beiden Gruppen. Aber wenn Impfungen wirklich ungesund sind, dann wäre auch zu erwarten, dass die Sterblichkeit/Menschenzahl bei jungen Menschen im Vergleich zu den Jahren vor der Pandemie und den Impfjahren gestiegen ist. Natürlich können auch hier Unterschiede durch andere Auswirkungen von Lockdowns usw. verursacht werden. Aber das scheint mir reiner zu sein als regelmäßige Messungen der Übersterblichkeit ... weil es viel mehr Annahmen erfordert, beispielsweise im Hinblick auf die Bevölkerungsstruktur. Während die heutigen 40er-Jahre beispielsweise einigermaßen mit den 40er-Jahren von vor ein paar Jahren vergleichbar sein sollten
Was Sie über die Übersterblichkeit sagen, scheint mit den Beobachtungen im Jahr 2021 übereinzustimmen. In diesem Artikel wird auch etwas über Altersgruppen gesagt. https://zorgkrant.nl/anders/14916-in-2021-10-procent-meer-oversterfte
Sie klingen („Annahmen“), als hätten Sie die Grafiken nicht gesehen oder würden sie in Frage stellen. Ich würde gerne hören, was daran falsch ist!
Tatsächlich ist die Sterblichkeit in jungen Altersgruppen besorgniserregender. Ich sehe in Ihrem Artikel nicht sofort irgendwelche Probleme. Ich glaube jedoch an das Experiment, weil es immer die Möglichkeit einer Verwechslung/eines Zufalls gibt, der dies erklärt. So bekommen zum Beispiel ungesunde Menschen häufiger eine Spritze oder Geimpfte gehen nach der Spritze ein höheres Risiko ein. Persönlich glaube ich nicht. Aber wir hätten größere, saubere Experimente mit langer (verblindeter) Nachbeobachtung durchführen sollen. Ich schätze, dass Pfizer mit 15.000 pro Arm und 15 Todesfällen in der Kontrollgruppe ungefähr die Macht hatte, eine Übersterblichkeit von 1/1000 signifikant zu messen. Das ist es also, was wir „wissen“. Allerdings ist eine um 1/3000 höhere Sterblichkeit aufgrund von Impfungen möglich. Bei Pfizer starben 6 von 15.000 weiteren (zumindest zitiere ich hier Norman Fenton)
Angesichts der Gesamtkonstanz über zwei Jahre erscheint mir ein Zufall schwierig. Ich habe die verwirrende Möglichkeit mit Statistikern und Datenanalysten untersucht. Natürlich ist es nicht auszuschließen, aber mögliche Erklärungen können den Effekt nicht quantitativ erklären. Welche Störfaktoren fehlen uns? Und diese sollten für alle Altersgruppen gelten, denn überall passiert mehr oder weniger das Gleiche... Ich freue mich über (einigermaßen gut durchdachte) Vorschläge.
Schöne Analyse. Sind Sie der Erste, der diese Analyse durchführt? Sie würden eine schnelle Antwort auf diese besorgniserregende Analyse erwarten. Warten sie, bis die Analyse pro Rezension veröffentlicht wurde, bevor sie antworten?
In fast allen westlichen Ländern ist ein Anstieg der „gesamten Übersterblichkeit“ zu beobachten. Da stimmt etwas nicht.
Lieber Anton,
Leider enthält dieser Artikel viele Fehler. Ich bin überrascht, dass Sie sagen, Sie hätten dies mit Datenanalysten und Statistikern besprochen. Vielleicht sollten Sie einfach einen Epidemiologen fragen, der sich mit Confounding auskennt, oder einen Demografen, der sich mit Altersstandardisierung auskennt. Diese Daten sind bereits in der Tabelle enthalten, und die ONS-Statistiker haben das bereits für Sie erledigt.
Erstens ist es falsch, den Impfstatus aus der zweiten Quelle zu beziehen. Das bedeutet, dass Sie mit zu großen Teilern arbeiten, da aufgrund der gesamten Gruppe in Quelle 2 im Jahr 2021 bereits Menschen gestorben sein müssen. Deshalb verwenden die ONS-Statistiker Raten – weil sie wissen, dass Menschen leben, weil sie zu den Tagen/Jahren des Lebens beitragen. Dies war ein allgemeines Problem der NIMS-Datenbank: Für junge Menschen wird die Gesamtbevölkerung überschätzt, da NIMS auf der Existenz einer Hausarztdatenbank basiert. Diese können doppelt bestehen, beispielsweise für Studierende und ausgewanderte Migranten.
Zweitens ist ein altersstandardisierter Satz ein Satz, der das Alter innerhalb der Alterskohorten korrigiert. Dies bedeutet, dass die Sterblichkeit in der Gruppe neu berechnet wird, wenn die Altersstruktur innerhalb dieser Gruppe gemäß einer sogenannten Standardpopulation unterschiedlich gewesen wäre. Das bedeutet eigentlich, dass Sie die Tabelle nicht verstehen – aber das stimmt tatsächlich mit dem Alter überein.
Wenn Sie dann die ASMRs verfolgen, werden Sie tatsächlich ein sehr klares Muster erkennen: Der ASMR der geimpften Gruppe ist (oft viel) niedriger als der der ungeimpften Gruppe. Die ASMR von Personen mit weniger als 3 Injektionen ist oft höher als die der ungeimpften Gruppe. Dieser Kontrast (viel niedriger geboostet, höher nicht geboostet) weist auf eine Verwechslung hin. Eine davon kommt in der Impfstoffepidemiologie recht häufig vor: die Voreingenommenheit gegenüber gesunden Impfstoffen. Mit anderen Worten: Menschen mit höherem Bildungsniveau bekommen eher eine Auffrischungsimpfung und haben einfach eine geringere Sterblichkeit.
Das andere ist verwirrend durch (Kontraindikation). Warum bekommen die Leute nicht ihre nächste Injektion (1. -> 2., 2. -> 3.)? Eine Erklärung des ONS hierfür ist, dass sich die Menschen in akuter Not befinden oder ihnen mitgeteilt wurde, dass sie eine unheilbare Diagnose haben. Dieser Unterschied war zu Beginn des Injektionsprogramms recht dramatisch und lässt nach einer Weile nach. Aber diese Dynamik kann sich für Menschen, die sich später für eine Impfung entscheiden, fortsetzen: Ihnen wird eine Diagnose gestellt, die sie nun in eine gefährdete Gruppe einordnet, und sie entscheiden sich für eine Impfung.
Warum schrumpft der Unterschied dann, wenn man die Trends im Laufe der Zeit betrachtet? Die Gruppe der Ungeimpften besteht einfach aus einer Gruppe von Menschen, die bereits Corona hatten. Der Unterschied in der durch Corona erklärten Sterblichkeit aller Ursachen verringert sich daher, insbesondere im Vergleich zur Basisreihe. Dies führt dazu, dass Menschen mit gefährdeten Komorbiditäten unter den Geimpften überrepräsentiert sind. Es ist daher durchaus zu erwarten, dass es bei Personen mit <3 Impfungen zu einer höheren Gesamtmortalität kommt als in der ungeimpften Gruppe.
Hallo Jaime,
Zunächst einmal: Vielen Dank für Ihre Zeit! Ich hatte eine lange Antwort vorbereitet, vielleicht können wir uns das zu gegebener Zeit noch einmal ansehen.
Das wichtigste Thema – und Sie sind nicht der Erste, der das vorschlägt – ist die Altersstandardisierung. Dies ist notwendig, um verschiedene Altersgruppen sinnvoll vergleichen zu können oder beispielsweise eine Sterblichkeitsrate für eine gesamte Bevölkerung zu berechnen. Es kann Unterschiede innerhalb einer breiten Altersgruppe erklären, wenn man Parameter einbezieht, die sich mit dem Alter ändern.
Ich sehe nicht, welchen Beitrag das hier leisten kann. Zum Beispiel: In der Gruppe der 80-89-Jährigen könnte man sagen: 85-89 hat eine höhere Sterblichkeitsrate als 80-84. Aber beide Untergruppen haben die gleiche Impfquote (95,9 % und 96 %), sodass das überhaupt nicht verzerrt ist.
Meine Frage ist also, welchen Beitrag die Altersstandardisierung hier leisten kann. Meiner Meinung nach (und Wissenschaftlern in meinem Bekanntenkreis): keine. Wie sieht das ein Epidemiologe?
Noch einmal, Anton, die Antwort liegt in den Quelldaten, die Sie selbst konsultiert haben. ONS liefert Ihnen die Nenner für die rohen Sterblichkeitsraten (sehen Sie sich einfach die relative Differenz zwischen Ihren Ergebnissen und den ONS-Berichten an) und dann die standardisierten Werte. Der Unterschied zwischen diesen ist der Effekt der Standardisierung.
Der Punkt ist nicht, dass es keinen Unterschied in den Impfraten gibt, der Punkt ist, dass es einen Unterschied in der Altersverteilung zwischen der geimpften und der ungeimpften Gruppe gibt. Sie müssen also eine Gewichtungskorrektur auf die Differenz anwenden. Standardisierung ist hierfür eine Standardmethode.
Es scheint mir offensichtlich, dass dies für die kleinen Unterschiede wichtig ist (ein RR von <1,5 ist ein kleiner Unterschied): Die Sterblichkeitsraten in der Bevölkerung steigen jedes Jahr um 10 %.
https://www.ons.gov.uk/peoplepopulationandcommunity/birthsdeathsandmarriages/lifeexpectancies/datasets/nationallifetablesenglandreferencetables
Wieder einmal meine Überraschung. Bei allen diesen Kennzahlen handelt es sich um Standarddemografien. Sie kommen nur aus der Quelle, die Sie konsultiert haben, und sie liefern einfach mehr erwartete Ergebnisse. Warum haben Sie sie ignoriert?
Korrektur: Teiler.
Wenn ich mir übrigens die Unterschiede zwischen den genannten Raten ansehe, fällt mir auf, dass sie sich innerhalb der Altersschichten kaum unterscheiden. Dies bedeutet, dass wir uns wieder mit einem altmodischen Problem mit den Sharern befassen, und wenn Sie dem britischen Twitter gefolgt sind, ist dies ein weithin bekanntes Problem: Es gibt zu viele Menschen in NIMS (63 Millionen, während England +/- 55 Millionen hat), und sie können nicht geimpft werden. Wenn diese nicht geimpft werden können, können sie nicht zur Sterblichkeit beitragen. Dies bedeutet, dass die Verwendung von NIMS als Nenner immer zu einer Unterschätzung der Mortalität in der geimpften Gruppe führt.
Die ONS-Raten stammen aus einem Datenlink, wie in der Quelle beschrieben: dem Public Health Data Asset, in dem es auch heißt, dass die Links offenbar nur für 80 % der Bevölkerung in England über 10 Jahren funktionieren.
Darüber berichtete die Financial Times bereits im Jahr 2021. https://www.ft.com/content/125fbaf8-175a-4e2e-852a-9995ca5176b2
Darin sind wir uns also nicht einig: „...dass es einen Unterschied in der Altersverteilung zwischen der geimpften und der ungeimpften Gruppe gibt.“
Beide Gruppen sind (im Beispiel) im gleichen Zeitraum zwischen 80 und 90 Jahre alt und stammen aus derselben Bevölkerungsgruppe. Warum gehen Sie davon aus, dass die Altersstruktur zwischen diesen beiden Gruppen unterschiedlich ist? Diese ungeimpften Menschen könnten (im Extremfall) alle unter 85 Jahre alt sein, meinen Sie das? Aber Sie sollten sehen, dass sich das in der Impfrate der 5-Jahres-Kohorten widerspiegelt und sie sich kaum voneinander unterscheiden.
Auf jeden Fall werde ich weiter schauen, vielleicht kann mir jemand erklären, warum eine Standardisierung auch dann notwendig ist, wenn man Kohorten isoliert behandelt. Meiner Meinung nach ändern veränderte Sterblichkeitsraten nicht das Verhältnis zwischen zwei Gruppen im Alter von 80 bis 90 Jahren. Aber nochmals vielen Dank für Ihren Beitrag und sicherlich auch für Ihre inhaltliche Herangehensweise.
Aus dieser NIMS-Datei habe ich nur die Prozentsätze verwendet, nicht die Bevölkerungsgröße. Diese Prozentsätze sind korrekt (ich hoffe es), sie werden pro Tag und pro 5-Jahres-Altersgruppe angegeben! Ich habe daraus keine absoluten Aussagen gemacht.
Ich habe die Arbeit bereits für Sie erledigt: Es gibt tatsächlich kaum einen Unterschied zwischen den berechneten Rohsätzen und den standardisierten Sätzen. Es bleibt bestehen, dass die von der ONS berechneten Raten das Gegenteil von dem zeigen, was Sie zeigen, und daher liegt ein Problem mit den Teilern vor (zumindest gehe ich davon aus, dass Sie dieselben Nenner verwendet haben).
Ich möchte mich nicht über Sie lustig machen und gehe davon aus, dass Ihre letzte Antwort zu voreilig war. Überdenken Sie, ob die Prozentsätze gleich sind, wenn sich der Divisor ändert. Sie müssen prüfen, wie es möglich ist, dass die ONS-Raten zu einer geringeren Sterblichkeit bei Menschen führen, die jemals geimpft wurden ...
Prozentsätze sind natürlich eine Division und die Nenner sind genauso wichtig wie die Zähler. Aber dann ist die Vax-Quote, die das Vereinigte Königreich in Quelle 2 meldet, im Wesentlichen falsch? Für die älteren Gruppen denke ich, dass sie sonst nie einen Prozentsatz über 85 % erreichen könnten.
Ich hatte auch gehört, wie sich Fenton über die Bevölkerungsgröße beschwerte. Es ist ein bisschen Chaos.
Und fangen wir nicht an, uns übereinander lustig zu machen, das passiert schon genug 😉 Ich habe angenommen, dass NIMS und ONS jeweils konsistent sind, damit ich die Verhältnisse verwenden kann – aber natürlich nicht den Zähler des einen und den Nenner des anderen. Obwohl das eigentlich möglich sein sollte. Ich werde mich dieses Wochenende damit befassen.
Ich möchte Ihnen versichern, dass die unabhängige Statistikbehörde PHE (jetzt UKHSA) gerügt wurde, weil sie Sterberaten auf der Grundlage von NIMS-Nennern gemeldet hat. Und auch der FT-Artikel, den ich oben gepostet habe.
https://osr.statisticsauthority.gov.uk/communicating-data-is-more-than-just-presenting-the-numbers/
Ich frage mich übrigens, ob das ONS genau untersucht hat, ob es mit seiner verknüpften Datendatei (der PHDA, die ich oben erwähnt habe) immer noch über eine repräsentative Stichprobe innerhalb der englischen Bevölkerung verfügt. Doch ohne viel zu wissen, würde es mich wundern, wenn dieses Verhältnis im Vergleich zum tatsächlichen Verhältnis von Vax/Non-Vax sehr verzerrt wäre. Mit NIMS ist dies gewährleistet, da die Gruppe konstruktionsbedingt zu groß ist.
Hallo Jaime, ich habe über den entsprechenden Artikeln eine Nachricht platziert. Es folgt ein Artikel (hoffentlich dieses Wochenende), in dem ich aufzeige, was mit den britischen Zahlen und damit mit den Grafiken nicht stimmt. Soweit ich sehen kann, liegt es nicht an Fehlern in der verwendeten Methode oder in den zugrunde liegenden Daten. Wie Sie selbst angeben, verwendet die ONS-Methode auch Daten, anhand derer etwas gefunden werden kann ...
Vielen Dank, dass Sie mich auf diese Spur gebracht haben.
Wir werden sehen. Aber ich möchte hier ein wenig klarstellen, dass ich im Hinterkopf ein wenig misstrauisch bin. Das ONS hat die Raten, die einfach stark mit den Todesfällen pro Kopf zusammenhängen, in der Tabelle angegeben. Tatsächlich sind die Raten besser, weil sie berücksichtigen, dass Menschen im Laufe der Zeit sterben und sich die Altersgruppen verändern.
Diese gehörten Ihnen, und dann hätten Sie gesehen, dass sich für jede Altersgruppe das Gegenteil von dem herausstellt, was Sie gefunden haben. Warum haben Sie Ihre eigene Analyse durchgeführt und Ihren Lesern nicht berichtet, was tatsächlich in der Tabelle steht, insbesondere angesichts der großen Diskrepanz? Ich habe Ihnen diese Frage jetzt wiederholt gestellt. Sie stellen die Angaben in Quelle 1 falsch dar, weil dort auch angegeben ist, wie viel (genauer: wie viel Exposition) es auf jeder Altersstufe gibt.
Hallo Jaime, diese Unterschiede zwischen den Altersgruppen sind offensichtlich und in diesen Grafiken geht es nicht darum. Es spielt keine Rolle. Eine Altersanpassung wird nicht vorgenommen, da dies bei diesem Design nicht erforderlich ist. Die Altersstandardisierung korrigiert nicht „innerhalb einer Altersgruppe“, daher korrigieren Sie Unterschiede zwischen Altersgruppen, wenn Sie sie statistisch vergleichen oder zusammenführen.
Ich hatte eine einfache Frage: „Wie ist die Vax/Onvax-Mortalitätsverteilung innerhalb jeder Altersgruppe?“ Die Einteilung in 5 Unterkategorien von Geimpften, die dann aufgrund von Zeitvorgaben und Altersangaben in Sterbewahrscheinlichkeiten und Personenjahre zurückgerechnet werden, wirkt dann eher verwirrend als klärend. Auch die Definition von „ungeimpft“ war ebenso unsicher. (In einigen Tabellen gilt: 1 Injektion = ungeimpft oder innerhalb von 21 Tagen nach der Injektion = ungeimpft).
Ich habe auch gesehen, dass in bestimmten Kategorien die Zahl der geimpften Personen die vom ONS geschätzte Bevölkerung überstieg. Das war für mich ein guter Grund, in eine andere Richtung zu blicken, mit den offiziellen Bevölkerungszahlen der Regierung. Meiner Meinung nach war die verwendete Bevölkerung falsch.
Ich hoffe, ich habe Ihre Frage jetzt klar beantwortet. Wahrscheinlich haben Sie Recht, wenn Sie misstrauisch sind: Ich bin tatsächlich jemand, der das Vertrauen in Institutionen und Regierungen völlig verloren hat. Ich habe so viele Ungenauigkeiten und unwissenschaftliches Verhalten von Gesundheitsinstituten, Regierungen und Universitäten gesehen, dass ich dazu neige, nicht zu glauben, was sie uns sagen.
Auch das habe ich in einem Artikel erklärt. Ich werde das ein paar Leute lesen lassen, bevor ich es poste.
Anton, dein Verdacht entbindet dich nicht von der Verantwortung, deinen Lesern einfach die Zahlen zu präsentieren, die von Leuten präsentiert werden, die nachweislich qualifizierter sind als du. Lese ich daraus nun, dass Sie von den Ergebnissen mit ONS-Nennern wussten und diese deshalb bewusst nicht dargestellt haben?
Auch hier sind ASMRs ein standardmäßiges demografisches Maß. Die Tatsache, dass Sie sie schwierig finden, ist Ihr Problem. Sie sind nicht so kompliziert: Sie wählen eine Standardpopulation mit einer bestimmten Altersverteilung. Dann nehmen Sie die Zahl der Todesfälle von Menschen in ihren 70ern und wenden einen Korrekturfaktor an, der der Differenz zwischen Ihrer eigenen Bevölkerung und der Standardbevölkerung entspricht. Wenn also in Ihrer Bevölkerung 10 % 70-Jährige sind und in der Norm 8 %, dann erhöhen Sie die Zahl der Todesfälle für die 70-Jährigen um 80 %. Dies wiederholen Sie für alle anderen Alterskategorien und haben dann einen einheitlichen Tarif.
Darüber hinaus konnte man der Tabelle einfach keinen einheitlichen Tarif entnehmen. Die Rate ist einfach ein besseres Maß, weil man im Mai 2022 offensichtlich nicht die gleiche Bevölkerungszusammensetzung hat wie im Februar 2021. Dieser Unterschied nimmt zu, je höher die Sterblichkeitswahrscheinlichkeiten in den jeweiligen Gruppen sind: Dann nimmt der Nenner in der Gruppe mit der höheren Sterblichkeit schneller ab. Wenn Sie dies nicht korrigieren, scheinen sich die Sterblichkeitszahlen zwischen den Gruppen zu schnell anzugleichen.
Und ja, es stimmt, dass es beim ONS, bei dem es sich de facto um eine Volkszählung handelt, mehr Geimpfte in der alten Gruppe gibt als bei der Volkszählung Anwesende. Dies besagt lediglich, dass Volkszählungen tatsächlich nicht präzise sind und alle Methoden letztendlich *Schätzungen* sind. Das bedeutet nicht automatisch, dass Sie einen Datensatz verwenden sollten, der darauf ausgelegt ist, keine Menschen zu übersehen (NIMS – dieser bestimmt den Versand von Impfeinladungen und daher gibt es einen hohen Schwellenwert für die Entfernung von Duplikaten), insbesondere wenn Sie bei einem normalen Ansatz an die Metadaten sehen würden, dass er 63 Millionen Menschen enthält. Das sind 7 bis 8 Millionen Menschen, die ungeimpft und unsterblich sind, und daher eine Überschätzung von mehr als 10 % im Vergleich zu den Volkszählungszahlen. Bei einer „realen“ Impfquote von 90 % sind mehr als die Hälfte der Ungeimpften unsterblich (schließlich gilt: Bei einem realen Nennerverhältnis von 90:10 rechnet man mit einem Nennerverhältnis von 90: >20).
Hier stellen Sie die Tabelle erneut falsch dar, da in der ONS-Tabelle auch einfach „jemals geimpft“ angezeigt wird. Darüber hinaus stimmt es einfach nicht, dass Geimpfte als Ungeimpfte abgestempelt werden. Dies ist für die Beurteilung der immunologischen Wirkung auf die Corona-Mortalität vollständig verantwortlich, nicht jedoch für die Gesamtmortalität. Und wenn Sie zu Fenton kommen: Er kann hoch und tief springen, aber seine Argumente sind nicht wirklich überzeugend. Die Tendenz zu gesunden Impfstoffen ist in der gesamten beobachtenden Impfstoffforschung weit verbreitet. Seine Analysen haben dies nicht im Entferntesten als Erklärung für den Unterschied in der Nicht-Covid-Mortalität zwischen Vax und Nicht-Vax „entlarvt“. https://twitter.com/_johnbye/status/1547325894913581056
Es gibt auch eine einfache, nicht gemessene Verwechslung mit gesunden Impfstoffen: Wenn Sie im Januar 2021 wegen etwas, das nichts mit Corona zu tun hat, im Krankenhaus liegen, haben Sie ein höheres Sterberisiko. Gleichzeitig werden Sie im Krankenhaus nicht geimpft. Darüber hinaus korreliert die Impfung stark mit dem sozioökonomischen Status. Eine niedrigere Nicht-Covid-Sterblichkeit, wenn man das Alter korrigiert, ist daher nicht verdächtig – sie wird durchaus erwartet.
ONS-Erklärung zur höheren Sterblichkeit von Menschen, die nur eine Injektion erhalten haben:
https://www.ons.gov.uk/peoplepopulationandcommunity/birthsdeathsandmarriages/deaths/bulletins/deathsinvolvingcovid19byvaccinationstatusengland/deathsoccurringbetween1januaryand31october2021
Danke für den öffentlichen Austausch, Jaime und Anton! Wie gerne würde ich mehr davon sehen! Vor allem in Gegenden, in denen ich nicht zu Hause bin. Ich freue mich auf die Fortsetzung.