In onderstaande grafieken zijn de populatiegegevens van NIMS gebruikt. Hierdoor worden de sterftepercentages onder ongevaccineerden, in elk geval in enkele leeftijdsgroepen, mogelijk lager weergegeven dan ze daadwerkelijk zijn.
Omdat Engeland met onzuivere populatieschattingen werkt, weten we niet hoeveel ongevaccineerden er zijn. De gehanteerde populatiegrootte heeft rechtstreeks effect op rapportage over ongevaccineerden. De afwijking verschilt bovendien per leeftijdsgroep. Het is nog niet duidelijk of en zo ja, hoe dit aangepast kan worden; het UKSHA (UK Health Security Agency) is hier wel mee bezig. Het ONS zegt hierover:
“We hopen dat het werk dat UKHSA doet om de NIMS-gegevens te verbeteren (inclusief het verwijderen van duplicaten), samen met het werk dat ONS doet aan bevolkingsschattingen en de volkstelling van 2021, ons inzicht zal verbeteren. Het is echt positief dat ONS en UKHSA samenwerken om te proberen een oplossing te vinden voor dit probleem, dat zo belangrijk is voor zo veel statistieken. Gezien deze onzekerheid kan kennis van de implicaties van de verschillende keuzes gebruikers helpen de gepresenteerde gegevens met de nodige voorzichtigheid te interpreteren.”
Uitgebreidere verantwoording vind je in de post “UK professor: ‘Data on mortality by vaxx status are junk’ “
Laten we hopen dat de de-duplicatie wordt uitgevoerd zonder met een half oog te kijken naar de effecten op de vaccinatie-effecten. Het organiseren van een onafhankelijke toezichthouder zou verstandig zijn (Prof. Fenton wil vast helpen) anders wordt het net zo’n krachteloze operatie als het oversterfte-onderzoek door CBS/rivm.
Hoe gaat het inmiddels in de landen die wél belangrijke cijfers openbaar maken? De data van UK zijn veelzeggend als ze in grafieken worden gezet. Die spreken voor zich, scroll gerust door. Er zijn verder geen correctie-methodes toegepast. Dat hoefde niet omdat er geen leeftijdsgroepen zijn getotaliseerd waardoor er bijvoorbeeld met person-years gewerkt moet worden. Zulke bewerkingen zijn noodzakelijk als er generaliserende uitspraken moeten worden gedaan over ‘de sterfte’. Nu we te maken hebben met een ziekte die bijzonder leeftijdsdiscriminerend werkt, heeft dat weinig zin. Het is juist zaak om de afzonderlijke leeftijdsgroepen in het oog te houden.
Er is één methodologisch probleempje: de sterfte wordt in 10-jaars cohorten gerapporteerd. Vooral tussen de 70 en 90 jaar zal dat betekenen dat er uitspraken kunnen worden gedaan over bijvoorbeeld 70-79, terwijl in de oudste groep 75-79 misschien wel drie keer zoveel sterfte is als in de jongste groep van 70-74. De rapportage is daarvoor te grofmazig. Dat is jammer – maar beter dan niets.
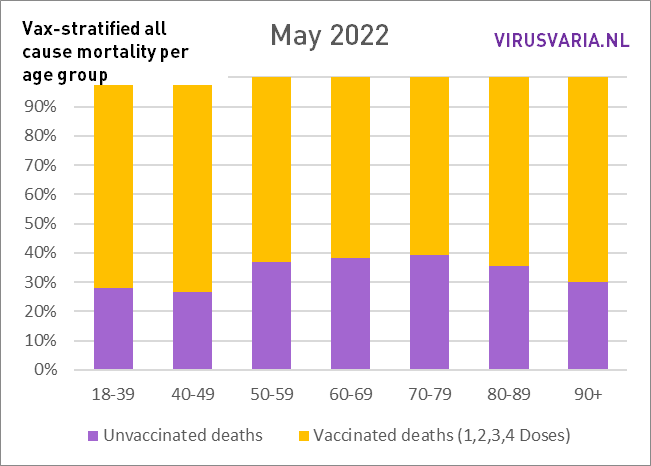
In hoeverre verschillen die 5-jaars ‘subcohorten’ eigenlijk van elkaar? Qua vaxpercentages zit er boven de 50 jaar in ieder geval weinig verschil (ca 2%) tussen de jongste ‘subcohorten’ en de oudste.
De vaxpercentages lopen op tot 95% bij de hoogbejaarden. Het is niet vol te houden dat de 5% ongeprikten toch al veel gezonder waren en daardoor voor lagere sterfte zorgen. Eerder omgekeerd: vrijwel iedereen zonder contra-indicatie is in die hogere leeftijdsgroepen geprikt.
Voor de jongere leeftijdsgroepen zou dat anders kunnen liggen maar daar is er weer veel minder verschil in sterfte (bijvoorbeeld tussen 40-44 en 45-49) dus daar speelt dat probleem nauwelijks. Het is er dus wel maar het verklaart de getoonde verschillen niet. Meer over de gevolgde methode en ‘confounding’ helemaal onderaan dit artikel.
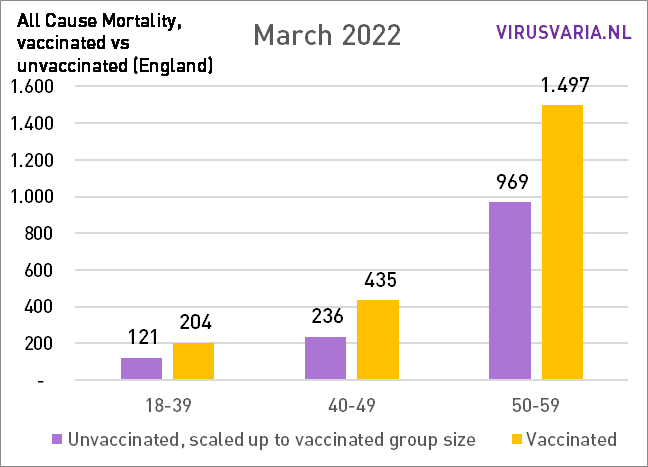
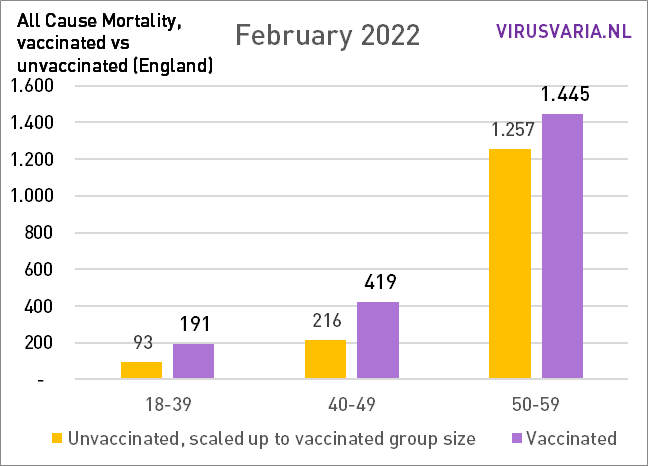
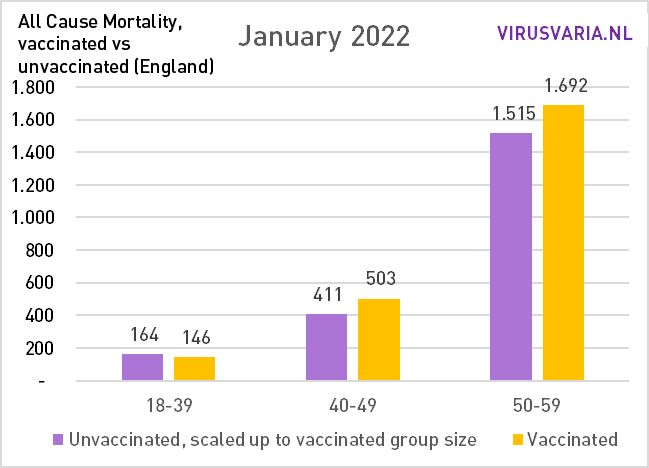
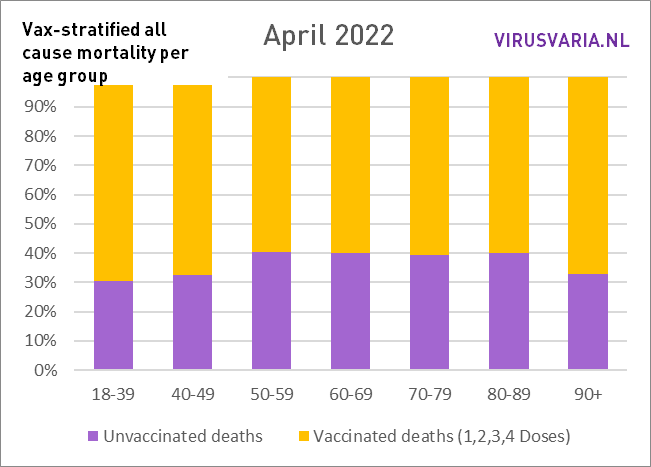
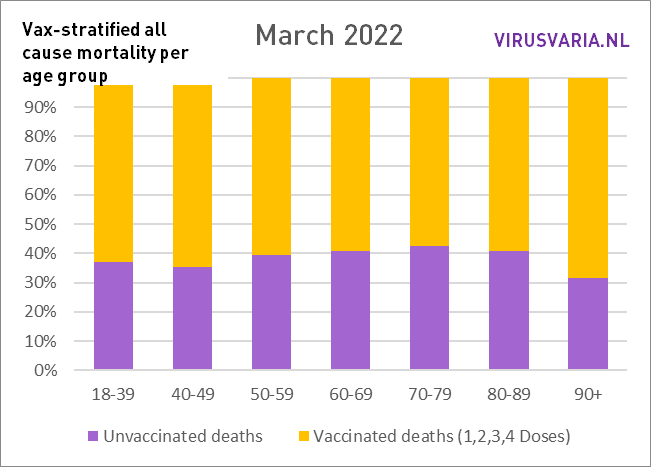
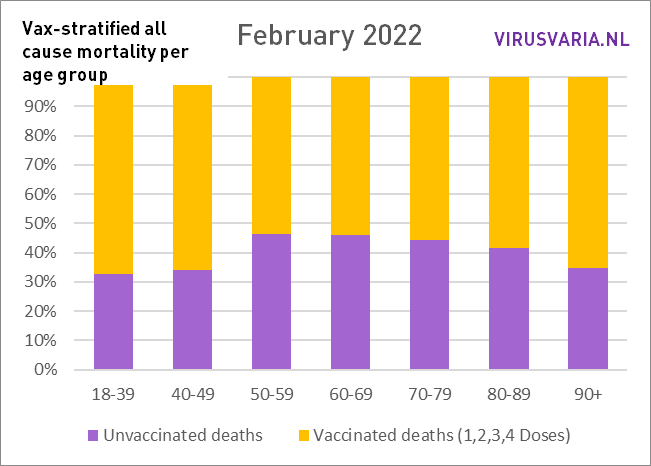
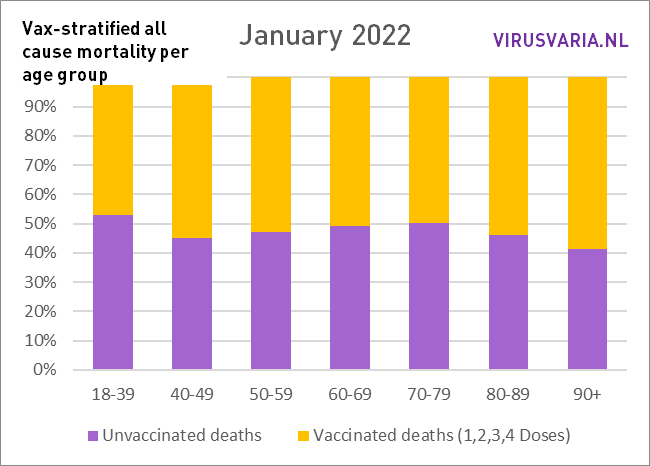
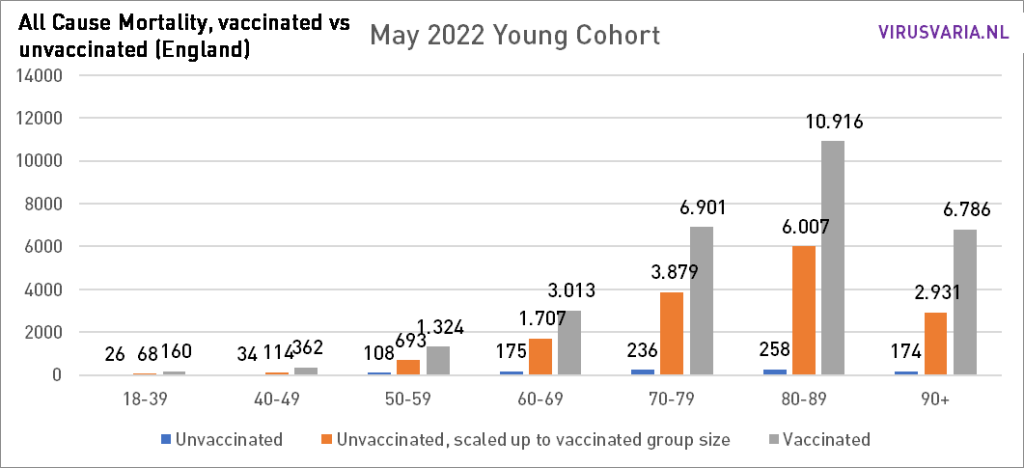
De grafieken zijn als volgt te lezen: de paarse staaf geeft weer hoeveel ongevaccineerden er zouden zijn gestorven als de groepen gevaccineerden en ongevaccineerden even groot waren geweest. Bij All Cause Mortality wordt géén onderscheid gemaakt in doodsoorzaken, dus het betreft zowel Covid als non-Covid sterfgevallen.
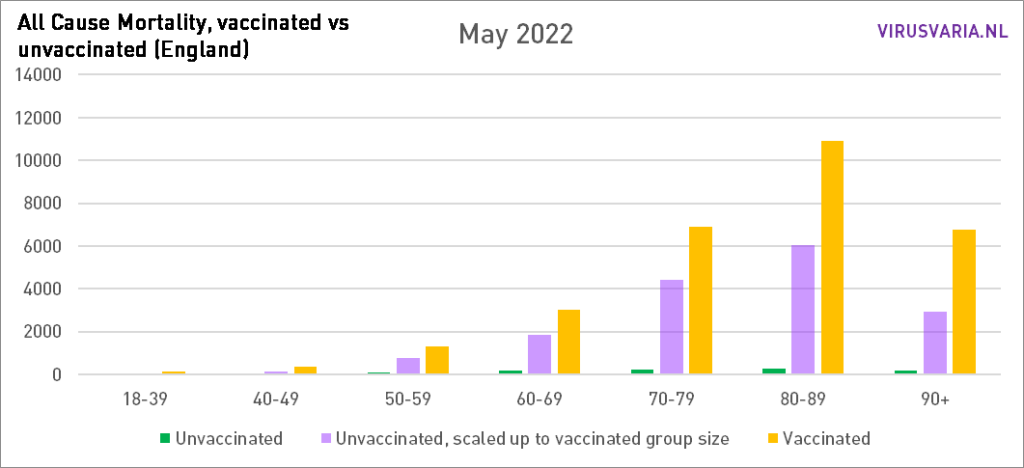
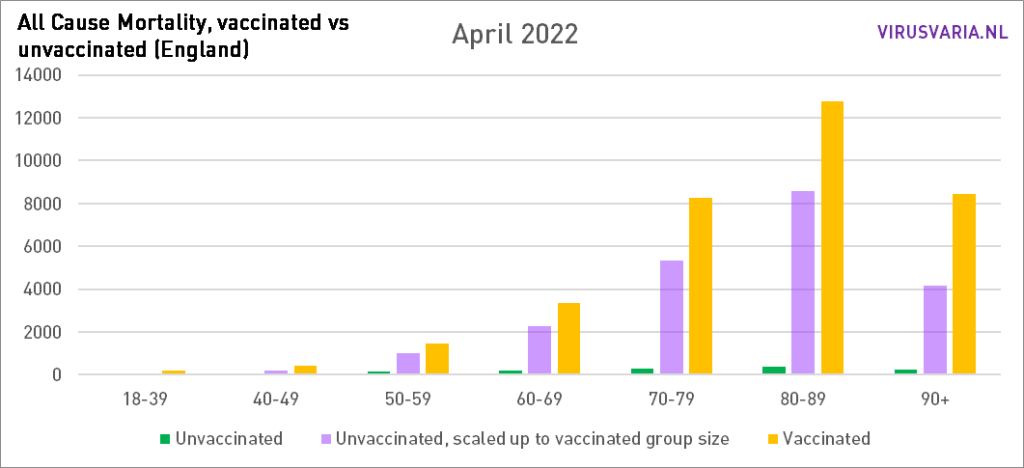
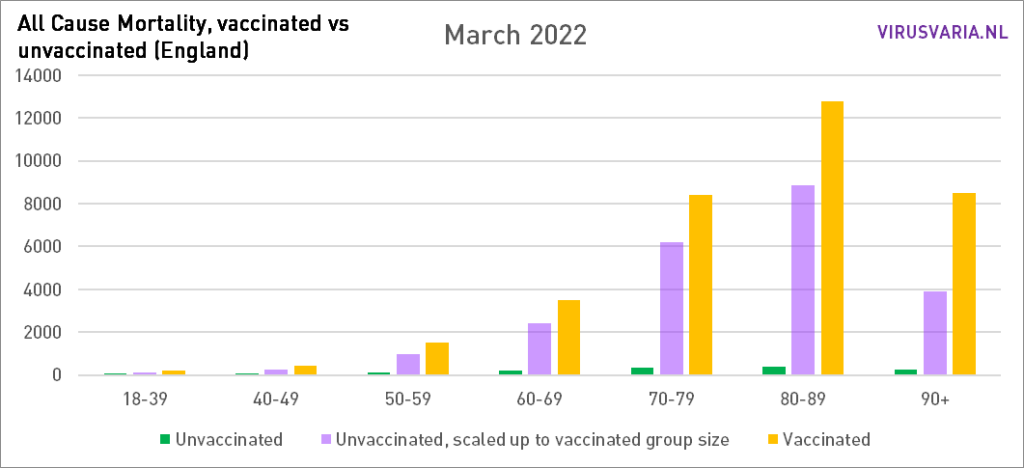
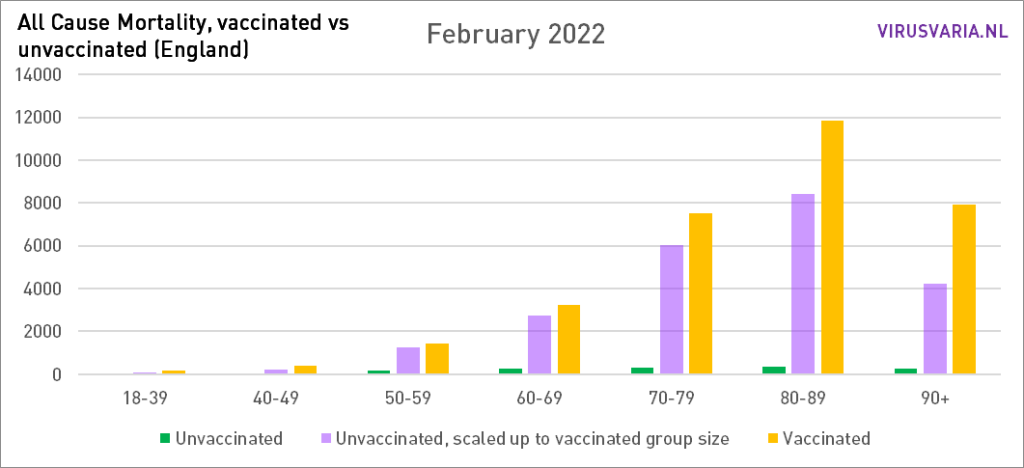
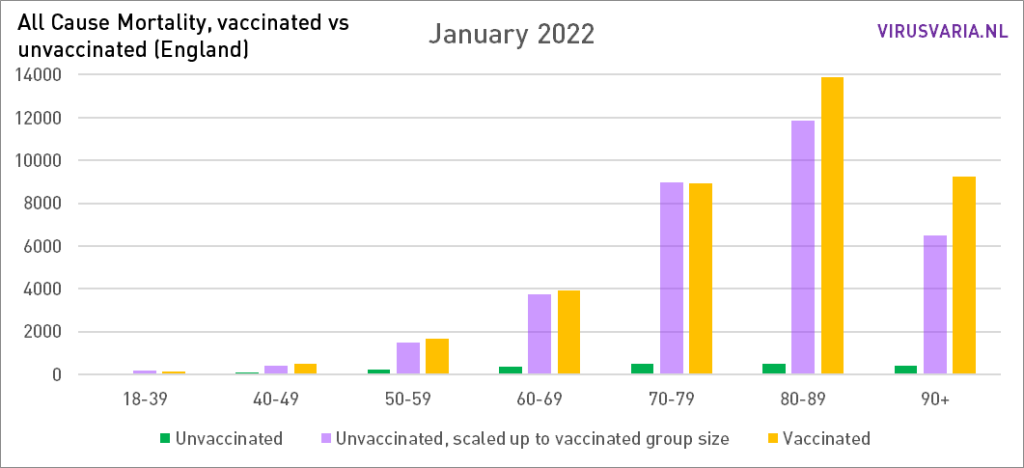
Grafieken 2021 staan hier.
Methode
Brondata van UK government:
1) Sterftecijfers naar vaccinatiestatus van gov.uk: download het Excel-bestand hier
2) Vaccinatiestatus (%) van gov.uk: download de XML-versie hier (knop onder de onderste grafiek)
Bron 1 geeft in groepen van 10-jaar (behalve de groep 18-39) weer hoeveel sterfgevallen er zijn geteld. Die worden opgesplitst naar ongevaccineerd, binnen 21 dagen na eerste dosis, na 21 dagen na eerste dosis, binnen 21 dagen na tweede dosis, na 21 dagen na tweede dosis, binnen 21 dagen na derde dosis, na 21 dagen na derde dosis. Wil je die subgroepen met elkaar gaan vergelijken dan wordt het erg ingewikkeld want tussen de eerste dosis en de tweede dosis zit veel meer tijd dan tussen de tweede en de derde – en dus zullen er alleen daarom al meer mensen overlijden. Om maar wat te noemen. Vandaar dat ik alle sterfgevallen bij elkaar heb opgeteld zodat ik het totaal aantal overleden gevaccineerden weet. Vervolgstudies kunnen dan op de details ingaan – voor zover dat interessant is bij een bloedbad als dit.
Bovenstaande gegevens over aantallen worden pas zinvol als we weten hoe groot elke subgroep is en hoe het met het vaccinatiepercentage van die groep zit. Dat staat exact in Bron 2. Helaas is die heel anders ingedeeld, in 5-jaars cohorten. Daarvan zijn eenvoudig 10-jaar cohorten te maken. Daarbij verliezen we wat resolutie maar om het andersom te doen wordt het soort trickery vereist waardoor het weer minder transparant wordt en je op een gegeven moment niet meer precies weet waarnaar je nou eigenlijk zit te kijken.
Verder worden de percentages per dag weergegeven terwijl de sterfte per maand gaat. De meest betrouwbare methode bleek om de 15e van elk maand als referentie te nemen. Vooral tijdens de campagnes was dat van belang. Inmiddels zijn de vaccinatiepercentages nagenoeg stabiel.
Dan hebben we van een leeftijdsgroep, waarvan we weten hoe groot die is, de vaccinatiestatus, bijvoorbeeld 80%. Dat betekent dat 20% ongevaccineerd. Je cijfers uit deze groep dus met 4 vermenigvuldigen om het rekenkundig naast de cijfers van de gevaccineerden te zetten. Een ander methode is om alles naar “per 100k” om te rekenen maar dan raken de verhoudingen soms weer zoek.
Dat is dus wat er is gedaan: in elke leeftijdsgroep is gekeken naar het aantal gestorven ongevacineerden (groen) en het aantal gestorven gevaccineerden (geel). Aan de hand van de vaccinatiegraad zijn beide groepen even groot gemaakt en het aantal doden is meegeschaald. Dat virtuele aantal wordt weergegeven door de paarse staaf.
Confounding
Binnen 10-jaar cohorts is er ook sprake van confounding. Het zou bijvoorbeeld zo kunnen zijn dat er tussen de 75-79 jaar veel meer mensen gevaccineerd zijn dan tussen 70-74 jaar. Als er dan ook meer mensen sterven in die oudere groep, lijkt het alsof ze sterven vanwege de vaccinaties. Helaas ontbreken de sterftegegevens per 5-jaars cohort. Wel zijn er de vaccinatiegraden. Boven de 70 jaar is het verschil binnen een cohort maximaal 1,5%. Het grootste verschil zit in het cohort 40-49: bijna 5%. (40_44: 77,02% en 45_49: 81,87% gevaccineerd).
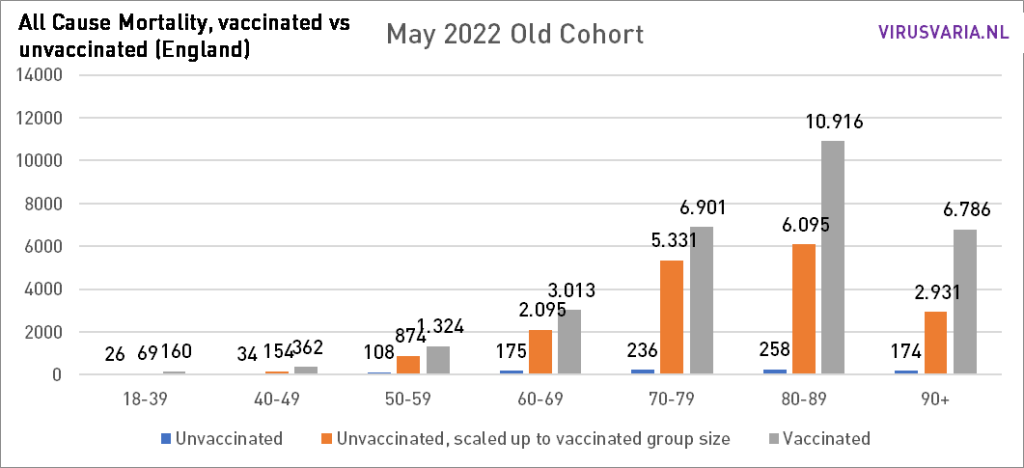
Om te zien hoe het qua vaccinatiepercentage enorm zou verschillen heb ik de hele maand mei ‘gedraaid’ met de vaccinatiegraad van het “jongere cohort’ en met die van het ‘oudere cohort’. Het grootste verschil is te zien in 70-79.
Als de verschillen beïnvloed zijn door confounding, hoop ik dat iemand mij kan uitleggen hoe de verschillen zo trendmatig kunnen veranderen. Om de trend te zien kun je alle grafieken vanaf begin 2021 hier bekijken.
Het blijft hoe dan ook ontluisterend.

Dank, Anton voor alweer goede uitpluizeriij. Vraag: worden mensen die nét (<3 weken?) voor het eerst gevaccineerd zijn meegeteld bij de ongevaccineerden?
Hallo Nanda,
Ze staan in de rapportage als ‘Overleden binnen 21 dagen na vaccinatie’. Ik heb ze daarom als ‘gevaccineerd’ behandeld. Ze worden gewoon zo geregistreerd daar. Ik begrijp de mensen niet die dat anders interpreteren. Ook als het om Covid/non-Covid gaat mag je die mensen niet als ongevaccineerd zien.
Ik begrijp wel dat ze ook apart geëvalueerd moeten kunnen worden.
Als ziekenhuizen alleen met de status ‘gevaccineerd: ja/nee’ werken creëren ze een probleem. Maar: Met wat goede wil kun je van elke overledene in het GGD-vaccinatieregistratiesysteem opzoeken op welke datum hij/zij is gevaccineerd. Als die wil er niet is en je moet leunen op ziekenhuisinformatie is het een chaos.
Het belang van die eerste drie weken: Bij artificiële immuniteit heeft het lichaam kennelijk drie weken nodig om bescherming op te bouwen die vier maanden stand houdt. Bij natuurlijke infectie heeft bijna iedereen na drie weken afgerekend met de ziekte en heb je robuuste immuniteit die minimaal net zo goed werkt en veel langer aanhoudt, in principe levenslang, als het virus niet muteert en zolang je immuunsysteem als zodanig nog goed werkt.
Het kan ook een strategie zijn zoals die is gebruikt bij HIV-behandelingen. Ging iemand ondanks behandeling met destijds experimentele medicijnen toch snel dood, dan was hij kennelijk al te verzwakt geweest en niet meer te redden. Zo werden veel ongelukken gemaskeerd, staat althans in The Real Anthony Fauci van Robert Kennedy jr. Ik ben dat voor waar gaan aannemen, ook omdat het boek wordt doodgezwegen.
Dank voor dit snelle en uitgebreide antwoord. Terecht dat je ze hebt geteld als gevaccineerd. Dat dit bij officiële cijfers niet gebeurde, heb ik altijd raar gevonden. Je telt dan m.i. de mensen die kort na de prik ws. aan die prik overlijden bij de verkeerde groep.
Mooi werk Anton!
Wat interessant is, is hoe lang de oversterfte van gevaccineerde blijft terugkomen in deze grafieken, wordt het verschil in 2022, 2023 kleiner? of blijft het zo groot voor de komende jaren?
In 2021 zeker in de begin maanden stierven er wel veel meer ongevaccineerde (feb, mrt, april ), Dus toen op korte termijn zou je kunnen interpreteren dat het vaccin zijn werk deed. Daarna zeg tot oktober 2021 ongeveer gelijk, en daarna stierven er meer gevaccineerde.
We gaan het zien!
Precies! Die eerste maanden zijn de reden geweest om stug door te blijven prikken (dat zie je ook in die eerdere post die ik nu heb geactualiseerd). Ondanks muterend virus en signalen van bijwerkingen.
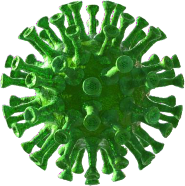
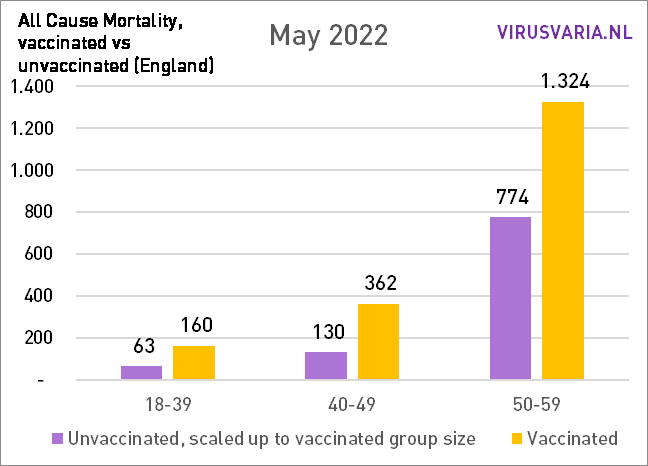
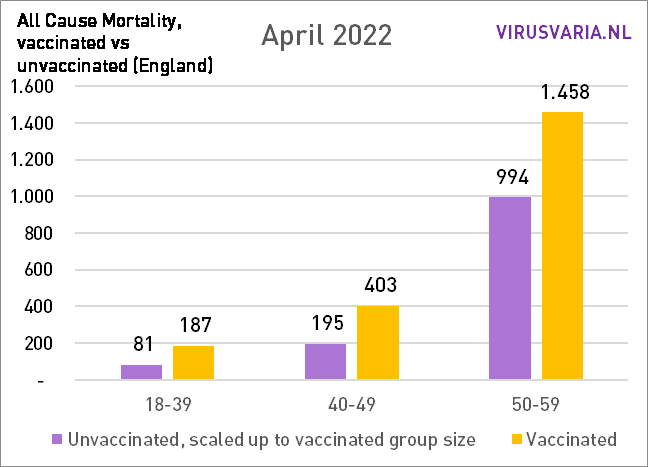
Het verschil tussen vax/unvax steeg tot nu toe. In onderstaande grafieken heb ik alle leeftijden bij elkaar opgeteld: de totale sterfte dus.
In mei is het verschil voor het eerst iets gedaald t.o.v. de maand ervoor, maar alleen in absolute zin!
De totale sterfte was ook lager in mei (ik vind het wel sterk fluctueren…) Percentueel is er daardoor géén daling, maar tnog steeds een stijgende trend.
Misschien wel de moeite om een artikeltje aan te wijden. Of twee: eentje met het goede nieuws en eentje met het slechte nieuws 😉
ik weet niet of je nog notificaties kijgt van een reply die ik ge-edit hebt. Vandaar even dit nieuwe antwoord. Ik gooi het zo weer weg. Groet, Anton
Hi Anton,
Ja ik krijg de replies! Alleen zijn we nu op reis, dus ik zit er iets minder bovenop…
Bedankt voor deze aanvulling. Ik ben geen medicus, er zullen absoluut factoren kunnen zijn die dit verschil gedeeltelijk kunnen verklaren, maar ik snap niet dat dit vaccin ingezet wordt voor Omicron, dat een andere ziekte lijkt als de eerdere varianten. Zowel qua verloop als qua werking van de vaccins.
Groeten Martin
Hoi Anton, dat vaccins niet veel (meer?) helpen om sterfte omlaag te brengen lijkt mij een redelijke aanname. Ondanks de mogelijke verschillen in bijvoorbeeld leeftijd en oorspronkelijke gezondheid tussen beide groepen. Maar stel vaccins zijn ook werkelijk ongezond dan zou je bij de jongeren ook verwachten dat de sterfte/personen gegroeid tov pre pandemie en vaccin jaren. Uiteraard ook daar kunnen verschillen veroorzaakt zijn door andere effecten van lockdowns e.d. . Maar dit lijkt mij zuiverder dan gewone oversterfte metingen…want daar zit veel meer aanname werk in mbt bijvoorbeeld bevolkinsopbouw. Terwijl de 40ers van nu bijvoorbeeld redelijk te vergelijken moeten zijn met de 40ers van een paar jaar terug
Wat je zegt over oversterfte lijkt wel te kloppen met wat er is geobserveerd in 2021. In dit artikel staat ook iets over leeftijdsgroepen. https://zorgkrant.nl/anders/14916-in-2021-10-procent-meer-oversterfte
Je klinkt (‘aannames’) alsof je de grafieken niet hebt gezien of in twijfel trekt. Ik hoor graag wat er niet aan deugt!
Inderdaad over sterfte over jonge leeftijdsgroepen is zorgwekkender. Ik zie zo direct geen issues in jouw stuk. Ik geloof echter in het experiment, want er is altijd een mogelijkheid op confounding/toeval die dit verklaart . Dus bijvoorbeeld ongezonde mensen worden meer geprikt of gevaccineerden nemen meer risico na de prik. Ik denk dit persoonlijk overigens niet. Maar we hadden grotere nette experimenten met lange (geblindeerde) opvolging moeten hebben. Ik schat dat Pfizer met 15.000 per arm en 15 doden in controle groep ongeveer de kracht had om extra sterfte van 1/1000 significant te meten. Dus dat is wat we “weten”. Maar 1/3000 aan extra sterfte door vaccins is dus mogelijk. Bij Pfizer stierven 6 op 15000 extra (althans ik quote hier Norman Fenton)
Toeval lijkt me gezien de overall consistentie over twee jaar een moeilijke. Ik heb de confounding mogelijkheid met statistici en data-analisten bekeken. Natuurlijk is het niet uit te sluiten maar mogelijke verklaringen kunnen het effect kwantitatief niet verklaren. Welke confounders missen we? En die zouden dan moeten gelden voor alle leeftijdsgroepen want overal gebeurt min of meer hetzelfde… Ik houd mij aanbevolen voor (enigszins doorgerekende) suggesties.
Mooie analyse. Ben je de eerste die deze analyse heeft gemaakt? Bij deze zorgwekkende analyse zou je toch wel snel een reactie verwachten. Wachten ze eerst met een reactie tot de analyse per reviewed is gepubliceerd?
In bijna alle westerse landen zie je een stijging van de “overall excess mortality”. Er is iets aan de hand.
Beste Anton,
Helaas zitten in dit artikel veel fouten. Ik verbaas me dat je zegt dat je dit met data-analisten en statistici hebt overlegd. Misschien moet je gewoon een epidemioloog vragen die verstand heeft van confounding, of een demograaf die verstand heeft van leeftijdsstandaardisatie. Die gegevens staan namelijk al in de tabel, en dat hebben de ONS statistici dus al voor je gedaan.
Ten eerste is de vaccinatiestatus uit de tweede bron halen foutief. Dit betekent dat je met delers werkt die te groot zijn, omdat van de hele groep in bron 2 er mensen in 2021 al moeten zijn overleden. Daarom gebruiken de statistici van het ONS rates- omdat men weet dat mensen leven, want ze dragen bij aan levensdagen/jaren. Dit was overigens een algemeen probleem met de NIMS database: voor jongeren wordt de gehele populatie overschat, omdat NIMS gebaseerd is op het bestaan van een huisartsenbestand. Deze kunnen dubbel bestaan voor bijv studenten en migranten die geëmigreerd zijn.
Ten tweede is een leeftijdsgestandaardiseerde rate een rate die corrigeert voor leeftijd binnen de leeftijdscohorten. Dit betekent dat de sterfte in de groep wordt herberekend als de leeftijdsopbouw binnen die groep anders was geweest, volgens een zgn. standaard populatie. Dit betekent eigenlijk dat je de tabel niet begrijpt- maar er wordt dus wel degelijk hiermee gecorrigeerd voor leeftijd.
Als je dan de ASMRs volgt, zie je eigenlijk een wel heel duidelijk patroon: de ASMR van de geboosterde groep is (vaak een stuk) lager dan de ongevaccineerde groep. De ASMR van de mensen met minder dan 3 prikken is vaak hoger dan de ongevaccineerde groep. Dit contrast (veel lager geboosterden, hoger niet-geboosterden) duidt op confounding. Eentje is vrij gebruikelijk in vaccinepidemiologie: healthy vaccineebias. Ofwel: hogeropgeleiden halen vaker een booster en die hebben gewoon lagere sterfte.
Het andere is confounding door (contraindicatie). Waarom halen mensen niet hun volgende prik (1e -> 2e, 2e -> 3e)? Een verklaring die het ONS hiervoor heeft gegeven is dat mensen acuut in de lappenmand zitten, of te horen gekregen dat ze een terminale diagnose hebben. Dit verschil was in begin van de prikprogramma vrij dramatisch groot, en na een tijdje zwakt dit af. Maar deze dynamiek kan voortborduren voor mensen die later beslissen een prik te halen: ze krijgen een diagnose te horen waardoor ze nu in een kwetsbare groep vallen, en besluiten een prik te halen.
Dan nog trendmatig in de tijd, waarom krimpt het verschil: de ongevaccineerde groep bestaat nu eenmaal uit een groep mensen die corona al heeft gehad. All cause mortality verschil dat verklaart wordt door corona verkleint dus, zeker in vergelijking met de basisserie. Dan blijft over dat in gevaccineerden mensen met kwetsbare comorbiditeiten oververtegenwoordigd is. Het is dus volstrekt verwacht dat voor mensen met <3 prikken er een grotere all cause sterfte is dan in de ongevaccineerde groep.
Hallo Jaime,
Allereerst: dank voor je tijd! Ik had een lang antwoord voorbereid, misschien dat we dat t.z.t. nog eens kunnen bekijken.
Belangrijkste onderwerp -en je bent niet de eerste die dat oppert- is de leeftijdsstandaardisering. Dat is noodzakelijk om verschillende leeftijdsgroepen zinnig te kunnen vergelijken of om bijvoorbeeld een mortaliteitsratio voor een hele populatie te berekenen. Het kan verschillen verklaren binnen een brede leeftijdsgroep als je tenminste parameters meeneemt die veranderen met de leeftijd.
Ik zie niet hoe dat hier kan bijdragen. Bijvoorbeeld: in de 80-89 groep zou je kunnen zeggen: 85-89 kent een hoger sterftepercentage dan 80-84. Maar beide subgroepen hebben dezelfde vaccinatiegraad (95.9% en 96%) dus dat vertekent helemaal niet.
Mijn vraag is dus welke bijdrage leeftijdsstandaardisering hier kan leveren. Volgens mij (en wetenschappers in mijn kennissenkring): geen. Hoe ziet een epidemioloog dat?
Nogmaals Anton, in de brondata die je zelf hebt geraadpleegd staat het antwoord. ONS geeft jouw de noemers voor de rauwe mortaliteitsrates (kijk maar eens wat het relatieve verschil is tussen wat jij hebt gevonden en wat ONS rapporteert) en daarna de gestandaardiseerde. Het verschil hiertussen is het effect van standaardisatie.
Het punt is niet dat er geen verschil is in vaccinatiegraad, het punt is dat er een verschil is in de leeftijdsverdeling tussen de gevaccineerde en de niet gevaccineerde groep. Je moet dus een weighting correctie toepassen op het verschil. Standaardisatie is een standaardmethode daarvoor.
Dat dit belangrijk is voor de kleine verschillen (een RR van <1,5 is een klein verschil) lijkt me evident: de mortaliteitsrates in de bevolking gaan met elk jaar 10% omhoog.
https://www.ons.gov.uk/peoplepopulationandcommunity/birthsdeathsandmarriages/lifeexpectancies/datasets/nationallifetablesenglandreferencetables
Nogmaals mijn verbazing. Al deze maten zijn standaarddemografie. Ze worden gewoon geleverd in de bron die jij hebt geraadpleegd, en ze geven gewoon meer te verwachten resultaten, waarom heb je deze genegeerd?
Correctie: delers.
Overigens lijkt inderdaad als ik het verschil tussen de genoemde rates kijk dat die binnen de leeftijdsstrata niet veel verschillen. Dat betekent dat we weer naar een ouderwets probleem kijken met de delers, en als je UK twitter had gevolgd is dit een al wel breder bekend probleem: in NIMS zitten teveel mensen (63 miljoen terwijl engeland +/- 55 miljoen telt), en die kunnen niet gevaccineerd worden. Als deze vervolgens niet gevaccineerd kunnen worden, kunnen ze ook niet bijdragen aan sterfte. Dat betekent dat NIMS gebruiken als deler altijd leidt tot een onderschatting van de sterfte in de gevaccineerde groep.
De rates van het ONS komen uit een datakoppeling, zoals omschreven in de bron: de public health data asset, waar gelijk ook staat dat de koppelingen kennelijk alleen lukken voor 80% van de bevolking in engeland boven de 10.
Financial times heeft hier al in 2021 over bericht. https://www.ft.com/content/125fbaf8-175a-4e2e-852a-9995ca5176b2
Hier zijn wij het dus niet over eens: “…dat er een verschil is in de leeftijdsverdeling tussen de gevaccineerde en de niet gevaccineerde groep.”
Beide groepen zijn (in het voorbeeld) tussen de 80 en 90 jaar, in hetzelfde tijdvak, uit dezelfde populatie. Waarom veronderstel je dat de leeftijdsopbouw verschilt tussen die twee groepen? Die ongevaxten zouden (in extremo) allemaal onder de 85 kunnen zijn, bedoel je dat? Maar dat zou je dan moeten terugzien in de vaxgraad van de 5-jaarcohorts en die ontlopen elkaar nauwelijks.
Ik zal in elk geval weer verder kijken, misschien dat iemand mij kan uitleggen waarom standaardisatie ook nodig is als je cohorten geïsoleerd behandelt. Veranderende mortaliteitsrates veranderen m.i. ook niets aan de verhouding tussen twee groepen van 80-90 jaar. Maar nogmaals dank voor je input en zeker ook je inhoudelijke benadering.
Van dat NIMS bestand heb ik alleen de percentages gebruikt, niet de populatiegrootte. Die percentages deugen (hoop ik dan toch), die worden per dag per 5j-leeftijdsgroep gerapporteerd! Ik heb daar geen absoluten van overgenomen.
Ik heb al zelf het werk voor je gedaan: er is inderdaad maar weinig verschil tussen de berekende rauwe rates en de gestandiseerde rates. Blijft staan dat de rates die het ONS uitrekent het omgekeerde laten zien dat jij laat zien, en dus is er een probleem met de delers (ik neem althans aan dat jij dezelfde noemers hebt gebruikt).
Ik wil je niet belachelijk maken en neem aan dat je laatste respons te snel gedacht is. Denk er nog eens over na of percentages hetzelfde zijn als de deler verandert. Je zult toch moeten gaan kijken hoe het kan dat de ONS rates komen op een lagere mortaliteit voor ooit gevaccineerden…
Uiteraard zijn percentages een deling en zijn de noemers net zo essentieel als de tellers. Maar dan klopt de vaxratio dus substantieel niet die UK rapporteert in Bron 2? Voor de oudere groepen toch wel, lijkt me, anders zouden ze daar nooit een percentage van boven de 85% kunnen halen.
Ik had Fenton ook al horen klagen over populatiegroottes. Een beetje chaos is het wel.
En laten we inderdaad niet beginnen met elkaar belachelijk maken, dat gebeurt al genoeg 😉 ik ging ervanuit dat NIMS en ONS elk op zich consistent waren dus dat ik de verhoudingen wel kon gebruiken – maar natuurlijk niet de teller van de een en de noemer van de ander. Al zou dat eigenlijk ook moeten kunnen. Ik ga er dit weekend in duiken.
Ik wil je ervan vergewissen dat de onafhankelijke statistiek autoriteit PHE (nu UKHSA) op de vingers heeft getikt voor het rapporteren van overlijdensrates op basis van NIMS noemers. En verder het FT artikel wat ik hierboven heb gepost.
https://osr.statisticsauthority.gov.uk/communicating-data-is-more-than-just-presenting-the-numbers/
Overigens vraag ik me wel af of de ONS goed heeft gekeken of met hun gekoppelde data bestand (die PHDA die ik hierboven noem) ze nog wel representatieve sample hebben genesteld binnen de engelse bevolking. Toch zou ik zonder veel te weten wel verbaasd zijn als dit een hele sterke scheve verhouding is ten opzichte van de echte verhouding vax/non vax. Met NIMS is dit gegarandeerd omdat de groep by design te groot is.
Hallo Jaime, ik heb een melding boven de betreffende artikelen gezet. Er volgt (ik hoop dit weekend) een artikel waarin ik aangeef wat er niet klopt aan de UK-cijfers en dus aan de grafieken. Het zit -voorzover ik kan zien- niet in fouten in de gevolgde methode alswel in de onderliggende data. Zoals je zelf al aangeeft gebruikt de ONS-methode ook data waar wat van gevonden kan worden…
Dank dat je me op dit spoor hebt gezet.
We zullen zien. Maar ik wil hier wel een klein beetje duidelijk maken dat ik in mijn achterhoofd een beetje achterdochtig ben. De ONS heeft de rates, die gewoon sterk gerelateerd zijn aan doden per hoofd van de bevolking, in de tabel aangegeven. Sterker nog, rates zijn beter omdat ze rekening houden met het feit dat mensen in de tijd overlijden en verschuiven van leeftijdsgroepen.
Deze lagen voor jouw voor het oprapen, en dan had je gezien dat het tegenovergestelde naar voren komt voor elke leeftijdsgroep dan wat jij hebt gevonden. Waarom heb je dan toch je eigen analyse gedaan en rapporteer je niet aan je lezers wat er eigenlijk gewoon in de tabel staat, zeker gezien de grote discrepantie? Ik heb je deze vraag nu herhaaldelijk gesteld. Je misrepresenteerd wat in bron 1 staat, want daar staat ook in hoe groot (preciezer: hoeveel blootstelling) er is op elk leeftijdsniveau.
Hallo Jaime, die verschillen tussen leeftijdsgroepen zijn vanzelfsprekend en daar gaan die grafieken niet over. Het doet niet terzake. Er wordt niet gecorrigeerd voor leeftijd omdat dat niet nodig is in deze opzet. Leeftijdsstandaardisatie corrigeert niet “binnen een leeftijdsgroep”, daarmee corrigeer je verschillen tussen leeftijdsgroepen als je ze statistisch vergelijkt of samenvoegt.
Ik had een simpele vraagstelling: “hoe is binnen elke leeftijdsgroep de sterfteverdeling vax/onvax?” De onderverdeling in 5 subcategorieën gevaccineerden, die daarna weer teruggerekend worden naar sterftekansen en persoonsjaren vanwege termijnen en leeftijden werkt dan eerder vertroebelend dan verhelderend. Ook was de definitie van “ongevaccineerd” even onzeker. (In sommige tabellen was 1 prik = ongevaccineerd of binnen 21 dagen na prik = ongevaccineerd).
Ik zag ook dat in bepaalde categorieën het aantal gevaccineerden groter was dan de door de ONS geschatte populatie. Dat was voor mij gegronde reden om in een andere richting eens verder te kijken, met de officiële populatie-aantallen van de overheid. De gebruikte populatie klopte m.i. niet.
Ik hoop dat ik je vraag nu duidelijk heb beantwoord. Je bent waarschijnlijk terecht achterdochtig: ik ben inderdaad iemand die zijn vertrouwen in instituties en overheden volkomen kwijt is geraakt. Ik heb intussen zoveel onjuistheden en onwetenschappelijk gedrag van gezondheidsinstituten, overheden en universiteiten voorbij zien komen dat ik de neiging heb om niet te geloven wat ze ons voorkoken.
Een en ander heb ik ook in een artikel uiteengezet. Ik laat dat aan een paar mensen lezen voordat ik het plaats.
Anton, je achterdochtigheid ontslaat je niet van de verantwoordelijkheid om gewoon aan je lezers de cijfers te presenteren zoals die door mensen die aantoonbaar meer gekwalificeerd zijn dan jij te presenteren. Lees ik nu hieruit dat je van de uitkomsten met ONS noemers wist, en dus bewust niet gepresenteerd hebt?
Nogmaals: ASMRs zijn een standaard demografische maat. Dat jij ze moeilijk vindt is jouw probleem. Zo ingewikkeld zijn ze ook niet: je kiest een standaardpopulatie met een bepaalde leeftijdsverdeling. Dan pak je het aantal doden van 70’ers, en past een correctiefactor dat het verschil is tussen je eigen populatie en de standaardpopulatie. Dus als in jouw populatie 10% 70’ers zijn, en in de standaard 8%, dan maak je het aantal doden voor de 70′ er 80% zo groot. Je herhaalt dit voor alle andere leeftijdscategorieën, en dan heb je een gestandaardiseerde rate.
Verder kon je uit de tabel gewoon niet gestandaardiseerde rate halen. De rate is gewoon een betere maat omdat je in mei 2022 natuurlijk niet dezelfde populatie samenstelling hebt dan in februari 2021. Dit verschil wordt groter naarmate de sterftekansen in de respectievelijke groepen groter zijn: dan daalt de noemer in de groep met hogere sterfte sneller. Als je hier niet voor corrigeert lijken de sterfte cijfers te snel naar elkaar te convergeren tussen de groepen.
En ja, het is zo dat de ONS, wat de facto een volkstelling is, meer gevaccineerden in de oude groep heeft dan die in de volkstelling aanwezig zijn. Dit zegt gewoon dat volkstellingen inderdaad niet precies zijn, en alle methodes zijn uiteindelijk *schattingen*. Dat betekent niet automatisch dat je een dataset moet gebruiken dat ontworpen is om geen mensen te missen (NIMS- dit bepaalt het uitsturen van vaccinatie uitnodigingen en is er dus een hoge drempel om duplicaten weg te halen) moet gebruiken, zeker als je met een normale benadering van de metadata zou zien dat er 63 miljoen mensen inzitten. Dat zijn dus 7 a 8 miljoen mensen die ongevaccineerd zijn én onsterfelijk, en dus >10% overschatting ten opzichte van volkstellingen. Bij een ‘echte’ vaccinatiegraad van 90% is meer dan de helft van de ongevaccineerden onsterfelijk (immers: waar de echte noemer ratio 90:10 is, reken je dus met een noemer ratio van 90 : >20).
Hier misrepresenteer je wederom ook de tabel, want ook de ONS tabel presenteert gewoon ‘ever vaccinated’. Daarnaast is het gewoon niet waar dat mensen die geprikt zijn als ongevaccineerd worden geturfd. Dat is voor het beoordelen van het immunologisch effect op coronasterfte volstrekt verantwoord, maar niet voor all cause mortality. En als je met Fenton aan komt zetten: hij kan hoog en laag springen, maar echt overtuigend zijn zijn argumenten niet. Healthy vaccine bias is zo’n beetje bonton in het hele observationele vaccinonderzoek. Zijn analyses hebben dit als verklaring in de verste verte niet ‘gedebunked’ als verklaring voor het verschil in non covid mortaliteit tussen vax en non vax. https://twitter.com/_johnbye/status/1547325894913581056
Er is ook simpele niet gemeten healthy vaccinee confounding: als jij januari 2021 in het ziekenhuis ligt voor iets wat niets met corona te maken heeft, heb je een hogere kans om te overlijden. Tegelijkertijd gaan ze jou in het ziekenhuis niet vaccineren. Daarnaast is vaccinatie sterk gecorreleerd met sociaal-economische status. Een lagere non-covid mortaliteit als je corrigeert voor leeftijd is dus niet verdacht- het is volstrekt verwacht.
Uitleg ONS over grotere sterfte mensen die maar 1 prik hebben gehaald:
https://www.ons.gov.uk/peoplepopulationandcommunity/birthsdeathsandmarriages/deaths/bulletins/deathsinvolvingcovid19byvaccinationstatusengland/deathsoccurringbetween1januaryand31october2021
Dank voor de openbare uitwisseling Jaime en Anton! Wat zou ik dat graag meer zien! Zeker op terreinen waar ik zelf niet in thuis ben. Ik zie uit naar het vervolg.