On 23 February, Statistics Netherlands (CBS) published figures that enabled us to calculate the effectiveness of the mRNA vaccines. It appears to have been virtually nil, as these figures show. In this article (in collaboration with Hans Verwaart) we explain. This article is also posted on LinkedIn. It is obvious that this article is considered displeasing by some readers of LinkedIn and may request that it be removed. That's why I'm calling on you to share this as much as possible.
On 23 February 2024, CBS published an article with the intention of showing that omitting the period up to 2 weeks after the second vaccination made little difference in the mortality picture. This is the article in question: Covid Vaccination Status and Mortality.
What's actually going on? Because the efficacy of the vaccines would not be up to par until 2 weeks after completing the primary treatment, you were only seen as "fully vaccinated" after these two weeks. That seems reasonable, but CBS has now adjusted this definition. But what else do the numbers in this report show? There was criticism of this approach, because there would also be many victims in those weeks after the 1st vaccination. We also see this in the graphs, but CBS does not pay any attention to it.
This is one of the graphs from Qatar who was supposed to show us the usefulness of vaccination:
This graph suggests that you are 68% protected from week 2 and 95% after the second shot. But is that really the case?

As we will see later, in the period between the 1st and 2nd vaccination (at least 4 weeks) there does not seem to be any decrease in mortality from covid-19. One explanation could be that the vaccine can only prevent mortality from an infection that occurs after the protection has been restored. Mortality then only occurs a few weeks after the infection, so with that explanation it is understandable that we do not see any effect in the first month after the first injection.
The government has also published about the need for the second jab. In Four reasons why your second coronavirus jab is not a luxury the government wrote that the second jab was desirable for several reasons, including "Without a second shot, the basic protection of the first shot decreases faster and is less good." So that basic protection was there, but not yet optimal, confusing. Also, an infection on the first day of vaccination will not yet have been stopped by the vaccine. But an infection after a week for the most part. 95% protection was promised, so an expectation of say 50% should be reasonable after the first vaccination, right? If it were to be reasonably stated that the first 4 weeks should be excluded from protection, then all the decrease in corona mortality can therefore be attributed to the build-up of natural immunity and vaccination mustard after meals.
CBS has decided to include the weeks after the second vaccination as "fully vaccinated" and has come up with an additional report. Changing this definition is not relevant to this article, but the availability of the intermediate counts is. The conclusion of CBS is as follows:
Using a different definition for vaccination status 'vaccinated', which does not take into account the waiting time after vaccination, results in a similar mortality picture for both COVID-19 and non-COVID-19 deaths as when the waiting period is included.
We take note of that. But now we can find out what the protection of the vaccine is in the period between the first and second vaccination. The tables provided by CBS enable us to calculate exactly what the effect of the first vaccination was, i.e. the risk of dying from covid-19 between the first and second injection. People who did not take a jab are therefore not taken into account, which is nice.
Experiment
If you wanted to know what the protection of the vaccine would be, you could set up an experiment for that. You divide the population into two groups, one part of which you vaccinate and the other part you don't, and you look at what the differences are. With a perfect vaccine, no one dies from covid-19 and with a non-working vaccine, there is no difference.
That experiment has already been conducted on a small scale and in a select group in the testing phase, which would suggest that the vaccine would have an efficacy of possibly 95%. But now for the practice. The experiment was not repeated without selection, it seems, but with the availability of the latest CBS figures, the experiment has been realized. We have to do the math for it.
Jip and Janneke
Because calculating with the CBS figures seems a bit complicated, first an explanation with an example in Jip and Janneke language.
Suppose you want to demonstrate that a vaccine has 100% efficacy. The entire population will be vaccinated over 20 weeks. You will give a second shot 4 weeks after the first shot and we will follow the part that has only received a first shot.
We look at the vaccination status of each death and we only count the deaths who have had exactly 1 shot. That's 20% of the population (4/20). If the jab does its job properly, there will be no one in that group who has died from the disease that the vaccine protects against. If the vaccine does nothing at all, then we find a number of deaths in this group that is also 20% of the total number of deaths from the disease. If the proportion were 10%, the vaccine would therefore protect for 50%. Etcetera.
Because the mortality risk strongly depends on age, we do not compare with the number of people within the group (i.e. 20% in this case) but with the total number of deaths within the group. This will sometimes result in percentages that are a little too high and sometimes a little too low, on average it will make little difference. If the vaccine would give 100% protection, it wouldn't matter at all.
This image is a visualization of the concept.

We assume that every 4 weeks 20% of the deaths are corona (the red dolls). There can sometimes be fewer (2) or more (3) deaths, but the mortality rate for corona is 20% in this calculation example. There can also be 5 weeks between 1st and 2nd injection (5), it doesn't matter for the chance. In (6) we see the situation if the vaccine has an effectiveness of 50% from day one. If the vaccine would only have an effectiveness of 50% from week 3, we would see the situation (7) and measure a VE of 25%. So everything is fictitious.
We are not looking for an exact percentage, but an indication of it. If we do want to know, we need more information about the ages at death. We have done that control calculation, but that makes the calculation too complicated for this article.
The Counts
The simplest part of the analysis is counting the differences in vaccinated deaths between the first and second shots. And we do that for both deaths from covid-19 and other causes of death. The CBS report contains four tables with the number of deaths per week. Here's an example of an excerpt from these tables:

There are four tables: two for deaths from covid-19 and two for deaths from other causes. Both broken down by whether or not Wlz (=Long-term Care Act, we will not make this distinction). The tables cover the years 2021-2022, but we will only look at the figures up to June 2021, after which there are hardly any first jabs, so we can no longer compare there. It should also be noted that a small proportion of the population (estimated at 7%) did not consent to the registration of vaccination status in the CIMS System. We will correct for that later.
Moreover, mortality from covid-19 had already been declining sharply from January 2021, even before the vaccines could have contributed to this. But certainly you can still calculate an effect that the vaccines would have given in preventing dying from covid-19.
However, CBS does show graphs up to and including the end of 2022, probably to suggest that including the waiting time makes little difference. This is one of these 4 charts:

In other words, there were Vaccinated deceased transferred to the group unvaccinated, which apparently caused fewer vaccinated people to die from covid-19, but also from other causes. So you will have to correct for that in any case.
The graph is intended to show that the 3 columns from the table will eventually arrive at the same value in 2022, but the information we need is precisely in the first part, where there is a difference between with and without waiting time.
Because we have both numbers (with and without waiting time) through this report, we can calculate how many more (or fewer) people died related to vaccination status.
Calculation method
The first step is to calculate the mortality per week between the 1st and 2nd vaccination. If we consider that group, we see the effect of exactly one vaccination. That number is the difference between the numbers in columns 2 and 3. So we now know how many vaccinated people died in each week from both covid-19 and other causes, who received exactly 1 dose.
We are now going to compare these figures with all deaths from covid-19 and other causes in the weeks in question. First, let's look at the numbers themselves.

In this graph, the total mortality from covid-19 for the vaccinated part of the population is shown as a green line. That's column 2 of the report. The red line is the total number of deaths from covid-19 according to the quarterly reports of Statistics Netherlands (CBS). We see here that the number of covid-19 deaths was already falling sharply from January, well before vaccination was introduced.
Due to the rising vaccination rate, the number of people who died of covid-19 despite the vaccination is of course also increasing, but some of all deaths would probably have been prevented by the vaccination. So we have to do the math for that.
How many vaccinations?
So the trick is to find out how large the vaccinated group was in those 4 weeks. For this, we can use the part of the total vaccinated mortality between the 1st and 2nd shot (the sum of all columns 2 minus 3).
We are now going to take advantage of the fact that the age distribution for covid-19 deaths is almost the same as for the total figures. We have already demonstrated this through a publication in ResearchGate.
So what we do is determine the ratio between the total number of deaths (all causes) of the first jabs and the total number of deaths that the CBS reports via the National Institute for Public Health and the Environment (RIVM) for the week in question in the entire population. So that's the vaccinated part of the population. This ratio is independent of the cause of death, but it does include the number of deaths from covid-19 itself. The percentage of people who have had one jab but not yet a second one fluctuates around 15%-20%.
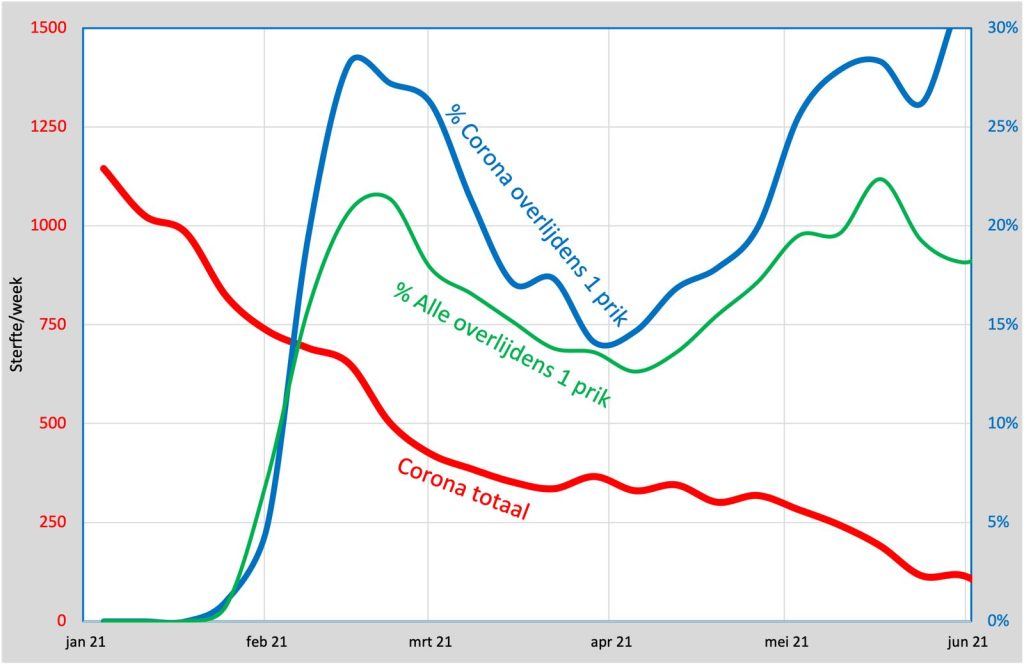
We also calculate the same ratio for deaths from covid-19. From the CBS tables, we again extract the weekly number of deaths from covid-19 between the 1st and 2nd jab (column 3-2 for covid-19 only) and divide that by the total number Deaths from COVID-19 in that week. We are correcting this by 7% due to the mentioned incomplete registration in CIMS. The following graph shows both percentages:
In this graph, a green line shows the percentage of vaccinated people who died between the 1st and 2nd shot. The blue line is the percentage of deaths from covid-19 during the same period, which should therefore be lower than the percentage for the entire group.
To our surprise, the percentage of deaths from covid-19 after vaccination is almost always higher than the expected percentage. Only in the first few weeks was it slightly lower, when healthcare workers in particular were vaccinated and no one died. There were 1251 deaths in the waiting period up to and including May, while the prognosis is 1001 deaths. This means that the protection of the vaccines is even negative, as much as -25%. And that is a completely different percentage from the 95% that we were promised.
From the end of May, the number of deaths from covid-19 decreases to such an extent that the statistics become unreliable. It is precisely this period with low mortality from covid-19 and high vaccination coverage that many analyses would show that the vaccines provided good protection. Small differences in vaccination rates and causes of death give a big bias!
Protection in 2022
After two more contagious variants appeared in 2021 (the British variant and the Delta), the reproduction number should have risen to around 5. This requires a herd immunity of at least 80%, which, according to the WHO, can only be achieved through vaccination. Because covid-19 mortality was already declining in January 2021, it seems as if that immunity had already been achieved, even before the vaccines were rolled out.
Indeed, we now have a vaccination rate of around 84% and that is cited by politicians as the reason that the pandemic has been successfully combated. Only unvaccinated people would then die from covid-19.
The CBS report should show that. However, nothing could be further from the truth! All we have to do is add up the deaths of the vaccinated and compare them with the total number of deaths reported by CBS.
In the report, we count 6518 vaccinated people who died from covid-19, while a total of 8432 deaths from covid-19 were registered in that year. Taking into account a vaccination rate of 84% and 7% underreporting, we arrive at a VE of only 8%. In other words, the unvaccinated group has a protection of at least 80% from natural immunity and the vaccinated group of 81.6%. Vaccination therefore provides an extra protection of no more than 1.6% for a disease that has already disappeared for at least 95%.
This protection does not yet take into account the "Healthy vaccine" effect, which means that healthy people are more likely to be vaccinated than people with a poor life expectancy and therefore die earlier unvaccinated. It is very likely that even that 1.6% will be undone.
Unwanted side effects
This is a separate story and cannot be determined with certainty. There is now an annual excess mortality of around 15,000 that can no longer be explained by mortality from covid-19. If it turns out that the vaccination is responsible for this, the calculated VE value will also be directly influenced and in a negative sense. So the value that is now at 8% could drop well below zero as a result. This analysis is worthy of a separate article.
Could we have known this before?
Yes, we could have known that as early as the spring of 2021. Every epidemiologist knows that vaccination contributes to lowering the reproduction number in proportion to vaccination coverage. So if you have vaccinated half of the population with a 100% effective vaccine, the reproduction number must also have been halved. This graph should show the effect of vaccination on the R-value from March onwards:
The reproduction number here is calculated on the basis of the mortality rates. It was just around 0.95 in January and even rose slightly to 1.0. But we don't see any drop in March that could be the result of vaccinations! Due to the seasonal effect, the reproduction number did not decrease until May, as can be seen in this graph.
The dotted line is the assumed course of the R-value if it would have been 95% effective from the second shot. We see that this was not followed and therefore there could not have been a significant effect of the vaccination.
Conclusion
By using the numbers in the report Covid Vaccination Status and Mortality we can calculate the protection that the vaccine would have given us during the 4 weeks after the first shot. It even turns out to be negative: -12%. This means that vaccination has actually increased the risk of death during the first 4 weeks after vaccination.
This method of calculation does not give a definite answer to what the protection was like in the following weeks, but it is not plausible that there would have been a clear increase in those weeks that would have been even close to the promised 95%.
Because the vaccine was only able to provide protection in March at the earliest, all the decline in covid-19 mortality until March can be attributed to the further build-up of natural immunity, as epidemiologists also know. Vaccination should have accelerated the build-up of immunity, but we are actually seeing a stagnation. Only the publication of the full dataset with a link between vaccination status and death (apparently CBS does work with this) can provide clarity on this.
In fact, the CBS mortality figures for 2022 show that the vaccines have provided (almost) no protection at all. Nevertheless, the minister has decided to hold a vaccination campaign again for 2024.
Calculation example
The calculations are difficult to follow from the story, so here is a calculation example.
We assume week 10, which is the week of March 8, 2021. So the numbers are coming out Covid Vaccination Status and Mortality, the total mortality from which the CBS reports via the National Institute for Public Health and the Environment (RIVM) and the mortality from corona from the quarterly reports of Statistics Netherlands (CBS).
We always take the figures for Wlz and nWlz together. The mortality between the 1st and 2nd injection is then (52-14) + (40-2) = 76 deaths from COVID-19 and (52-14) + (40-2) + (566-351) + (264-18) = 537 Total deaths with 1 vaccination.
The total number of deaths in week 10 is 3245 and the number of deaths within the 1 vaccinated group in that week was 537, or 537/3245 = 16,6%.
According to Statistics Netherlands, 423 people died of covid-19 in that week, which would result in 0.1655 X 423 = 70 deaths if vaccinated without the effect of vaccination. We assume that 7% of the vaccinated did not register (we have come across that number a number of times), so the expected value is for the number of deaths in week 10 that were vaccinated once 65. The percentage of 1 vaccinated death from covid-19 is therefore 65/423 = 19,3%.

I don't quite understand it yet. Maybe you can answer my question.
On the CBS site you can find the following:
Quote
'Vaccination status 'vaccinated' is defined as 'fully vaccinated' (i.e. two weeks after two approved vaccinations, or a positive test at least 56 days before at least one approved vaccination, or four weeks after vaccination where one vaccination counts as fully vaccinated according to the vaccination certificate, or when a booster or repeat vaccination has been administered without a known basic series) possible with boosters and repeat vaccinations. Vaccination status 'unvaccinated' is defined as no vaccination known or only one vaccination known without previously reported infection (with the exception of the vaccine where one vaccination counted as fully vaccinated).
Unquote
My question: People with 1 'vaccination' are therefore considered unvaccinated according to the CBS method. Only with a 2nd shot (infections aside) is the stamp 'vaccinated' put on. The only thing that has changed is the period after that. Then you miss people who died after the first injection and therefore never got around to a second one, don't you? Or is that information actually in the CBS tables?
This is only about the injections that had to be administered 2 times. The mRNA basically. AZ was a one-off.
I think the answer lies in this (Herman is offline for a while):
"As we will see later, in the period between the 1st and 2nd vaccination (at least 4 weeks), there does not seem to be any decrease in mortality from covid-19. One explanation could be that the vaccine can only prevent mortality from an infection that occurs after the protection has been restored. Mortality then only occurs a few weeks after the infection, so with that explanation it is understandable that we do not see any effect in the first month after the first injection."
(That also applies to those two weeks 'just pricked' after that, I think.)
There's something else. I looked at the CSV on twitter which is the basis. Here's any number of lines:
2022,46,2022-11-20,33,243,059,427,8,707,0,17,T,T,fully vaccinated with delay
2022,47,2022-11-27,22,215,025,404,4,529,0,14,T,T,fully vaccinated with delay
2022,48,2022-12-04,43,362,089,634,5,559,0,14,T,T,fully vaccinated with delay
2022,49,2022-12-11,42,431,124,737,10,1693,0,36,T,T,fully vaccinated with delay
2022,50,2022-12-18,55,504,195,812,7,1007,0,23,T,T,fully vaccinated with delay
2022,51,2022-12-25,80,1017,532,1503,12,1169,0,25,T,T,fully vaccinated with delay
2022,52,2023-01-01,70,519,25,788,14,1168,0,24,T,T,fully vaccinated with delay
2021,1,2021-01-10,0,0,0,0,636,4838,3933,5742,T,T,immediately after first dose
2021,2,2021-01-17,0,0,0,0,597,4784,3844,5725,T,T,immediately after first dose
2021,3,2021-01-24,0,0,0,0,591,4375,3501,5248,T,T,immediately after first dose
2021,4,2021-01-31,8,1985,0,44,468,4253,3306,52,T,T,immediately after first dose
2021,5,2021-02-07,32,1266,259,2273,378,4234,3199,527,T,T,immediately after first dose
2021,6,2021-02-14,109,2241,1212,327,281,4474,3266,5682,T,T,immediately after first dose
2021,7,2021-02-21,155,2644,1492,3796,194,2784,1878,369,T,T,immediately after first dose
2021,8,2021-02-28,107,1471,717,2225,115,1712,985,244,T,T,immediately after first dose
2021,9,2021-03-07,72,935,366,1505,92,1598,867,2329,T,T,immediately after first dose
2021,10,2021-03-14,52,493,141,845,77,177,928,2611,T,T,immediately after first dose
2021,11,2021-03-21,27,288,0,6,67,2702,1375,4029,T,T,immediately after first dose
2021,12,2021-03-28,39,267,092,441,47,1044,486,1602,T,T,immediately after first dose
2021,13,2021-04-04,14,151,0,3,43,1959,822,3096,T,T,immediately after first dose
2021,14,2021-04-11,17,141,013,269,38,1769,582,2956,T,T,immediately after first dose
2021,15,2021-04-18,21,223,0,4,35,16,507,2692,T,T,immediately after first dose
2021,16,2021-04-25,11,064,0,1,27,1509,294,2723,T,T,immediately after first dose
2021,17,2021-05-02,15,174,0,3,37,1339,334,2344,T,T,immediately after first dose
2021,18,2021-05-09,21,21,0,4,24,1243,255,223,T,T,immediately after first dose
2021,19,2021-05-16,17,194,009,379,25,2133,546,372,T,T,immediately after first dose
2021,20,2021-05-23,16,183,0,4,15,1181,0,24,T,T,immediately after first dose
2021,21,2021-05-30,4,086,0,2,10,508,0,11,T,T,immediately after first dose
A description is therefore 'immediately after first dose'. I would like to understand the underlying data. This phrase seems to indicate that CBS may have shared more than intended?
Source: https://pastebin.com/raw/RvG4gyve
"But what else do the numbers in this report show? There was criticism of this approach, because there would also be many victims in those weeks after the 1st vaccination. We also see this in the graphs, but CBS doesn't pay any attention to it."
That's what you mean I guess.
AZ Vaxzevria was also a double dose. Not mRNA but adenovector simian vaccine, with a piece of rhesus (macaque) monkeys in it. https://www.cbg-meb.nl/onderwerpen/medicijninformatie-vaccinaties/coronavaccins/covid-19-vaccin-astrazeneca
I see it now. They did take it with them. 'without waiting period, after first vaccination'. I think that's the category 'immediately after first dose'.
Perhaps a suggestion to add a short description of the underlying data to the introduction? For me, at least, it wasn't entirely clear. Now it is.
Assume that this article is under attack from all sides. So it's better to align everything clearly.
I wonder if CBS deliberately published the number of deaths after the first vaccination, or was it a mistake? Pretty lethal mistake (pardon the pun).
Many people have already delved into the data internationally. This cannot be reversed.
Nu stop ik. Bedankt voor deze analyse weer.
Another addition to Anton's explanation: CBS makes a confusing distinction between "vaccinated" and "fully vaccinated". Vaccinated was 2 weeks after the first shot, you were fully vaccinated 2 weeks after the 2nd shot (or 4 weeks after the 1st if there was only 1 shot). Now it is the case that you are fully vaccinated immediately after the 2nd shot.
But for the analysis, changing the definition doesn't matter at all. However, as a "service", CBS has thought to show that changing the definition makes little difference by publishing the intermediate counts. And we can now put them to good use.
I do not rule out the possibility that CBS felt cornered and sent a message with this publication that was actually forbidden.
They're in quicksand. They sink deeper and deeper. And if they move to want to do something about it, it only gets worse. Only finishing from the outside will be offered solace. But then they have to ask for help. As it looks now, they prefer to drown ... And are even prepared to drag the entire community along with them. Bunch of sad people.
What I don't understand at all regarding the effectiveness of the vaccine is the fact that at the end of 2021 and the beginning of 2022, hospitals were overcrowded with corona patients. In some countries Canada, Denmark, Cyprus, Japan, Australia, Israel etc. there were more corona patients than ever before. The vaccine is said to prevent hospitalization and death. When I quote the figures from Our World in Data, I am told to take into account the number of unvaccinated people and put the numbers in context. I am of the opinion that the vaccine does not prevent hospitalization at all, especially because some of the unvaccinated will also have built up immunity through infection. Is my thinking wrong or do I have to take into account a number of additional factors before drawing conclusions? Thank you in advance for your response.
Those are our thoughts too. You'll also see it from February 2021. Hospitalizations began to rise at the time of vaccination
In addition: the reason that all those people have been admitted as unvaccinated is caused by the largest Covid smokescreen, also mentioned above; The fact that people are only seen as vaccinated 2 weeks after the 2nd shot. This has been applied worldwide. As Professor Norman Fenton has pointed out, this is how you can make the greatest poison seem safe and effective. After all, anyone who dies from it or becomes ill from it within 6 weeks is considered unvaccinated. The solution? Vaccinate even more, of course. A vicious circle.
I don't think the uncritical narrative followers know this. This is despite the fact that it is (or was) on the RIVM site.
This simple, unquestionable fact should be known to everyone.
This article is a missed opportunity.
This is because the same mistake is made as with the RIVM analyses about the start of the vaccinations: nothing can be said about the efficacy of the vaccination with simple statistical techniques because there are far too many disturbing factors.
The definition of vaccinated/unvaccinated is just one of those confounding factors. Other factors are: downward trend epidemic after peak at the end of 2020, order of vaccination based on vulnerability/age groups, seasonal effects and special effects such as the 'healthy vaccinee' effect. All these kinds of effects must first be filtered out of the mortality figures, or made the analysis more specific (e.g. by age group) in order to really come to conclusions about the efficacy of vaccines in the period up to June 2021. Lumping all deaths together during this period is not productive.
It would have been more convincing to visualize the effects of the definitions on the basis of previous analyses by RIVM and CBS of the effectiveness or effects with some of our own, stylized example calculations and pictures.
Furthermore, I couldn't easily reproduce the 8% effectiveness in 2022. Could you elaborate on that? It became clear to me during my attempts that the calculation is very sensitive to the assumption of 7% underreporting. That is also somewhat alarming.
We turn the numbers we have inside out and squeeze them to the last drop. We look forward to hearing your method and data so that we can work more accurately.
Over die 8%: dat soort lage percentages schieten al gauw alle kanten op, je moet er niet teveel waarde aan hechten.
Er komt morgen of overmorgen een nieuw artikel waarin de VE wat preciezer wordt berekend.