Wir sehen regelmĂ€Ăig Prognosen, die darauf hindeuten, dass die Ăbersterblichkeit vorbei ist. Dabei liegen immer wieder fehlerhafte KohortenzusammenfĂŒhrungen zugrunde, aus denen dann falsche Schlussfolgerungen gezogen werden.
Dieser Artikel kann auch weitergelesen werden Website von Herman Steigstra.
Ein Beispiel, entnommen aus einem Rechenbeispiel eines Kritikers. Vereinfachte Zahlen fĂŒr eine kleine Kohorte aus drei Altersgruppen mit drei unterschiedlichen Sterblichkeitswahrscheinlichkeiten (10 %, 20 % und 30 %). Eine hypothetische Situation im Jahr 2019 und im Jahr 2024:

Wir konzentrieren uns auf die Sterblichkeit bei 80-JÀhrigen. Das Sterblichkeitsrisiko betrÀgt 20 % und es spielt keine Rolle, ob wir dieses Sterblichkeitsrisiko im Jahr 2019 oder im Jahr 2024 betrachten. In diesem Beispiel gehen wir davon aus, dass dieses Risiko aufgrund einer besseren Gesundheit oder anderer Ursachen nicht abnimmt. Basierend auf dem Sterblichkeitsrisiko berechnen wir auch die Anzahl der TodesfÀlle pro Altersgruppe in den Jahren 2019 und 2024.
Wir gehen dann davon aus, dass uns die Zahlen fĂŒr 80 Jahre nicht vorliegen, sondern dass diese nur als zusammengesetzte Kohorte von 79-81 Jahren vorliegen. AnschlieĂend schĂ€tzen wir das Sterblichkeitsrisiko fĂŒr einen 80-JĂ€hrigen als Durchschnitt der drei Kohorten im Alter von 79 bis 81 Jahren.
Im Jahr 2019 zÀhlten wir somit 262.000 Einwohner dieser Kohorte und insgesamt 49.600 TodesfÀlle. Wenn wir das aufteilen, sehen wir ein Sterblichkeitsrisiko von 18,9 %, was deutlich unter den 20 % liegt, die wir bei 80-JÀhrigen sehen. Nur durch die Verschmelzung mit den beiden angrenzenden Zeitaltern.
Im Jahr 2024 werden wir die Populationen fĂŒr 79 und 81 Jahre vertauschen. Wir verzeichnen mittlerweile mehr TodesfĂ€lle als im Jahr 2019, wĂ€hrend die Gesamteinwohnerzahl und die Sterblichkeitsraten gleich bleiben. Das durchschnittliche Sterblichkeitsrisiko der Kohorte ist mittlerweile gestiegen. Das Ergebnis dieser Sterblichkeitswahrscheinlichkeit hĂ€ngt also von der Verteilung der Populationen innerhalb der Kohorte ab.
Wie es sein sollte
Im Jahr 2023 haben wir diesen Artikel veröffentlicht: Eine Analyse der Ăbersterblichkeit basierend auf Alter und Geschlecht; die mögliche Rolle von Covid-19âŠHier beschreiben wir die Berechnungsmethode anhand von Trends, die auf Basis von Bevölkerungszahlen und SterbefĂ€llen, jedoch pro Alter und Geschlecht berechnet werden. Dies ist nun die Grundlage fĂŒr das, was wir NormmortalitĂ€t genannt haben.
Die Berechnungen wurden damals mit einem linearen Modell durchgefĂŒhrt, daher gehen wir davon aus, dass die Abnahme (oder vielleicht die Zunahme) des Sterblichkeitsrisikos proportional zu dem Jahr ist, fĂŒr das wir die Erwartung berechnen. Dies ist fĂŒr einen begrenzten Zeitraum noch in Ordnung, da sich die Sterblichkeitsraten nur langsam Ă€ndern. In zehn Jahren sehen wir einen RĂŒckgang von rund 20 %. Doch eines Tages wird sich der Niedergang noch weiter verlangsamen oder vielleicht sogar zum Stillstand kommen mĂŒssen, schlieĂlich werden wir nicht unsterblich. Deshalb wurden die Trendlinien nun durch ein Exponentialmodell ersetzt. Die Unterschiede scheinen gering zu sein, aber dennochâŠ. Als Beispiel die Sterblichkeitsrate im Alter von 50 Jahren:
Wir sehen hier, dass das Sterblichkeitsrisiko im Laufe von 20 Jahren (2000â2019) langsam von etwa 0,35 % im Jahr 2000 auf 0,2 % im Jahr 2020 abnimmt. Wir sehen auch, dass die Trendlinie leicht gekrĂŒmmt ist, was auf das Exponentialmodell zurĂŒckzufĂŒhren ist, das wir jetzt verwenden. Aber es ist minimal. Es ist wichtig, dass wir sehen, dass das Sterberisiko langsam sinkt.
Gleichzeitig mĂŒssen wir uns darĂŒber im Klaren sein, dass es sich bei dieser Grafik um eine einzelne Alterskohorte von nur 50-JĂ€hrigen handelt. Dies bedeutet, dass andere Kohorten Ă€lter werden nicht anwendbar, dies betrifft nur TodesfĂ€llekans. Ein gegenlĂ€ufiger Trend, da aufgrund der Alterung die Sterblichkeitsraten der Gesamtbevölkerung steigen, wĂ€hrend theoretisch jede 1-Jahres-Kohorte einen sinkenden Trend aufweisen könnte.
Alle Altersgruppen zusammen
Wir können nun die Gesamtzahl der TodesfÀlle in einem Diagramm im VerhÀltnis zur Trendlinie der Sterblichkeit von 2010 bis 2019 darstellen. Hier ist diese Grafik:
Die schwarze Linie wird anhand der erwarteten Sterblichkeitswahrscheinlichkeiten basierend auf allen 1-Jahres-Trends 2010â2019 berechnet. Die jĂ€hrlichen TodesfĂ€lle passen daher gut in diese Linie.
Im Jahr 2009 kam es zu einer Umkehr des RĂŒckgangs der Sterblichkeitsrate. Nach einer sinkenden Sterblichkeitsrate, insbesondere ĂŒber dem 50. Lebensjahr, stabilisierte sich die sinkende Sterblichkeitsrate auf etwa 2 % pro Jahr. Wir sehen dies in dieser Grafik: Die sinkende Sterblichkeit geht aufgrund einer alternden Bevölkerung in einen Anstieg ĂŒber.
Jetzt basierend auf Jahreszahlen pro 100.000
In diesem Schritt vereinfachen wir unsere Berechnung, wie es viele tun. Wir verwenden die Gesamtzahlen pro Jahr und rechnen sie in Sterblichkeit pro 100.000 Einwohner um, ĂŒblicherweise abgekĂŒrzt mit âpro 100.000â. Es entsteht dann dieser Graph:
Wir sehen, dass die Punkte im Vergleich zur vorherigen Grafik ungefĂ€hr gleich sind, und das ist richtig. Vor allem der MaĂstab ist unterschiedlich. Allerdings ist die Grafik auch leicht geneigt, da die Bevölkerung langsam wuchs. Im Jahr 2019 gab es 10.000 TodesfĂ€lle mehr als im Jahr 2000, aber pro 100.000 gerechnet waren es fast gleich viel. Bevölkerungswachstum und Alterung waren die Ursache. Es gab 1,4 Millionen Einwohner mehr.
Die durchgezogene Linie ist wieder die gleiche Basislinie wie in der vorherigen Grafik, wiederum verlÀngert bis 2030 unter Verwendung geschÀtzter Populationen nach 2025.
Aber dannâŠ
Falsche Modelle
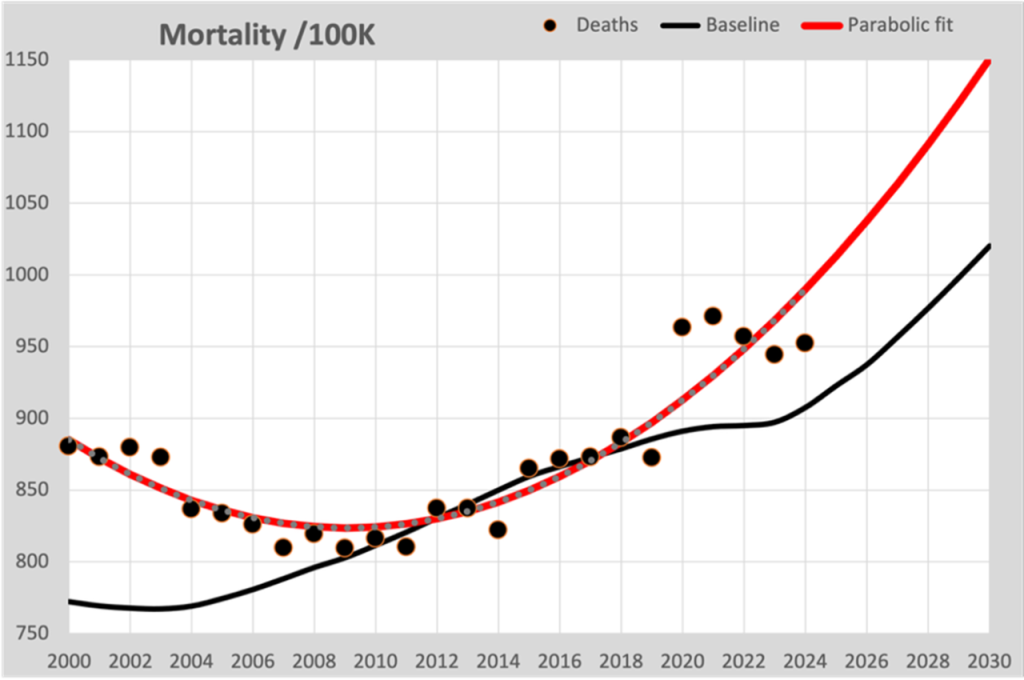
Viele Heimrechner gehen davon aus, dass man durch die 100.000 Punkte bis einschlieĂlich 2019 eine Kurve anpassen kann, die den Verlauf nach 2020 vorhersagt.
In diesem Diagramm ist die parabelförmige Anpassungslinie jetzt in Rot eingezeichnet, wie Sie es in vielen Diagrammen sehen. Hier gehen zwei Dinge schief:
- Die angepasste Kurve folgt (unabhÀngig vom gewÀhlten Modell) hauptsÀchlich den Zahlen, die sich aus dem Bevölkerungswachstum ergeben, und nicht der erwarteten Sterblichkeitsrate. Die Anspielung auf 2020 wird so sehr vermisst.
- Der RĂŒckgang der Sterblichkeit von 2000 bis 2010 verleitet sie dazu, sich fĂŒr ein parabolisches Modell zu entscheiden, das auch die Zahlen weit vor 2010 beschreibt. Die Folge ist, dass fĂŒr die Zukunft ein zunehmend steilerer Anstieg der Sterblichkeit vorhergesagt wird.
Wenn die bekannten Zahlen zur Bevölkerungszusammensetzung nicht berĂŒcksichtigt werden, muss die Linie an diese sich Ă€ndernden Zahlen angepasst werden. Es ist daher eine falsche Annahme, dass die Umrechnung in TodesfĂ€lle pro 100.000 Einwohner diesen Effekt neutralisiert.
Gute Modelle
Da es immer noch keine stabile Gesundheitslage gibt, mĂŒssen wir fĂŒr die Zahlen ab 2020 eine âbeste SchĂ€tzungâ prognostizieren. Wir können die Prognose weitgehend auf der Bevölkerungszusammensetzung basieren, da CBS sie jedes Jahr veröffentlicht. Die groĂe Unbekannte sind natĂŒrlich die erwarteten Sterblichkeitsraten. In unserem Berechnungsmodell gehen wir davon aus, dass die tatsĂ€chlich erwartete Sterblichkeit eine Fortsetzung des Trends ist, den wir bis 2019 gesehen haben. Auch CBS deutet seit langem an, dass sie nach diesem Prinzip arbeiten. Die Gesamtzahlen von CBS und unserem Standard-MortalitĂ€tsmodell stimmten bis 2022 sehr gut ĂŒberein.
Gute Modelle gehen daher von individuellen Sterblichkeitswahrscheinlichkeiten fĂŒr jedes Alter und Geschlecht aus. Diese Sterblichkeitswahrscheinlichkeiten zeigen eine zeitliche Entwicklung. Das gewĂ€hlte Modell bestimmt, wie gut die Fortsetzung gewesen wĂ€re, wenn es keine âunerklĂ€rliche Sterblichkeitâ gegeben hĂ€tte. Auch ist noch unklar, ob sich das, was uns seit 2020 widerfahren ist, auf das langfristige Sterblichkeitsrisiko auswirkt. Es kann sogar sein, dass es Gruppen von Menschen gibt, die von dem, was wir noch nicht wissen, nicht betroffen sind. Vielleicht erfahren wir in den nĂ€chsten Jahren mehr darĂŒber.
ASMR
Der ultimative Weg, VerĂ€nderungen in der Bevölkerungszusammensetzung auszugleichen, ist die ASMR (Altersstandardisierte Sterblichkeitsrate). Die Sterblichkeitsraten werden auf eine Standardpopulation umgerechnet. In unserem Fall wĂ€hlen wir die Bevölkerungsstruktur von 2019, die letzte ohne den Einfluss des âgroĂen Unbekanntenâ. Auf diese Weise ĂŒberfĂŒhren wir auch die Baseline in die Zahlen des Jahres 2019. Dies ist die beigefĂŒgte Grafik:
Dies ist sozusagen das Sterberisiko, wenn sich die Bevölkerungszusammensetzung nicht verĂ€ndert hĂ€tte, also nicht altern wĂŒrde. Obwohl wir diese Zahlen nicht direkt mit der tatsĂ€chlichen Sterblichkeit vergleichen können, geben sie doch einen guten Einblick in die Entwicklung der Sterblichkeitserwartungen. Wie bei der Sterblichkeitserwartung fĂŒr 50 Jahre in der ersten Grafik ist auch hier der gleiche RĂŒckgang zu beobachten, berechnet fĂŒr alle Einwohner nach der ASMR-Methode. Und das Wichtigste: Hier sehen wir die Ăbersterblichkeit ab 2020. Ohne jegliche Alterungseffekte. Wer also das Altern als Ursache fĂŒr ĂŒbermĂ€Ăige Sterblichkeit anfĂŒhrt, kann anhand dieser Grafik erkennen, dass es nichts mit dem Altern zu tun hat.
Wahl der Geschichte und des Modells
Eine lineare Trendlinie ist fĂŒr lĂ€ngere ZeitrĂ€ume ungeeignet, da selbst die sanfteste KrĂŒmmung eine zunehmende Diskrepanz zwischen Erwartung und RealitĂ€t erkennen lĂ€sst. Deshalb haben wir uns nun fĂŒr ein exponentielles Berechnungsmodell entschieden. Dabei wird davon ausgegangen, dass die Sterblichkeit jedes Jahr um einen festen Prozentsatz sinkt.
FĂŒr einen lĂ€ngeren Bezugszeitraum wird manchmal eine Parabel gewĂ€hlt, die bis 2020 einen RĂŒckgang und dann einen Anstieg zeigt. Wenn man in der Lage sein will, dieser Kurve weiter in die Zukunft zu folgen, stehen demografische Unmöglichkeiten im Weg, wie zum Beispiel eine anhaltende Beschleunigung der Sterblichkeit, eine unwahrscheinliche Entwicklung.
Allerdings zeigen die Punkte ab 2000 auch eine klare RegelmĂ€Ăigkeit, die formalisierbar zu sein scheint. Die beste Anpassung finden wir in einer logarithmischen Progression, die nahezu nahtlos mit den Punkten 2000 bis 2019 ĂŒbereinstimmt. Es ist durchaus vertretbar, dass wir diese Linie vorerst beibehalten können; es fĂŒhrt nicht zu unmöglichen Szenarien. TatsĂ€chlich stĂ€rkt es die GĂŒltigkeit der exponentiellen Linie von 2010 bis 2019, da beide Linien ab 2014 praktisch gleich sind.
SchlĂŒsse
Die Prognose fĂŒr die voraussichtliche Entwicklung ab 2020 hĂ€ngt stark von der Wahl des Berechnungsmodells und dem gewĂ€hlten Zeitraum ab, mit dem das Modell gespeist wird. Wir sehen diese Optionen:
- Linear von 2010-2019. Veröffentlicht in Researchgate. Scheint die erwartete Sterblichkeit gut zu beschreiben und liefert eine Prognose, die gut zu den CBS-Zahlen passt.
- Exponentiell von 2010 bis 2019. Ergibt fast die gleichen Zahlen, ist aber auf lange Sicht etwas realistischer.
- Parabolisch. Bietet auch eine gute Beschreibung fĂŒr die Jahre 2000-2010, prognostiziert aber einen starken Anstieg ab 2020, das ist eine Wahl.
- Logarithmisch. Ein Trend, der zwar nicht durch einen physikalischen Hintergrund untermauert wird, aber den Zahlen aus den Jahren 2003-2019 auffallend Àhnlich ist.
Fazit: Nur das Berechnungsmodell, das eine Parabel als Modell annimmt, sagt einen Sterblichkeitstrend voraus, der ab 2020 zwangsweise ansteigen wird. Dies fĂŒhrt ab 2022 zu einer Untersterblichkeit. Die anderen drei Modelle sagen ab 2014 allesamt einen nahezu exakt gleichen Verlauf voraus. Die ersten beiden passen sehr gut zu biologisch erklĂ€rbarem Verhalten. Letzteres funktioniert auch sehr gut, ist aber eher eine optische und numerische Passung als eine demografische oder biologische Untermauerung.






Gutes Modell, natĂŒrlich vier!
Dabei wird davon ausgegangen, dass in einer normalen Situation die Sterblichkeit in den meisten Altersgruppen von Jahr zu Jahr um einen bestimmten Prozentsatz abnimmt. Vorteil: Die Sterblichkeit kann nie unter 0 fallen.
Dies ist sicherlich eine Verbesserung gegenĂŒber dem zuvor veröffentlichten Artikel. Obwohl es leider zwangslĂ€ufig einige Spekulationen gibt. Aber es macht auf jeden Fall Sinn. Allerdings ist nicht auszuschlieĂen, dass der realistischste Trend auch ohne Corona und ohne mRNA im Jahr 2019 einen Wendepunkt erreicht hĂ€tte, weil unsere Sterblichkeit ohnehin schon so verdammt niedrig war. Aber lassen Sie uns diese Diskussion fĂŒr einen Moment beiseite legen ...
Die 1. Grafik mit ihren Schwankungen macht mich noch neugieriger auf die Zahlen fĂŒr 2025.
Denn liegen 50-jĂ€hrige MĂ€nner auf oder sogar unter der blauen Trendlinie? SchlieĂlich ist ihre Abweichung von der Linie im Jahr 2024 nicht gröĂer als in den Jahren 2002-2006, 2008, 2012 und 2014: die ânatĂŒrlichen Schwankungenâ.
Und wie werden Frauen im Jahr 2025 aussehen? ZurĂŒck auf Kurs oder dauerhaft erhöht?
Das Fazit lautet vorerst:
â Frauen mit 50 = ein Problem
â MĂ€nner von 50 könnten wieder auf dem richtigen Weg sein
Ich bin daher wieder einmal sehr gespannt auf die Grafiken von 2010 â 2024, in denen man alle Schwankungen pro Jahr und pro Alter sehen kann, und nicht nur die Werte von 2019 und 2024 wie im vorherigen Artikel. Denn diese stĂ€rker vergröĂerte Grafik, die nur die 50-JĂ€hrigen, aber alle Jahre zeigt, veranschaulicht schön, dass es in all den Jahren einige Schwankungen gab.
Aber vielleicht wird das keine wesentlichen neuen Informationen/Einsichten liefern ... Vielleicht werden diese Grafiken wiederkommen? Mir geht es auch gut, wenn sie erst 2026 zusammen mit den Zahlen von 2025 kommen.
P.S. Schön, dass Sie mein extremes (völlig unrealistisches) Zahlenbeispiel, inspiriert von Hermans, verwendet haben, um den Bevölkerungswachstums- und Alterungseffekt von 21,1/18,9 = 11,6 % auf die Sterblichkeit von 80-JĂ€hrigen fĂŒr jedermann glasklar zu veranschaulichen.
Vielen Dank fĂŒr Ihre Antwort Jan. Alle Zahlen finden Sie ĂŒber die Excel-Tabelle, die wir in dem Artikel veröffentlicht haben, den wir dazu geschrieben haben:
https://steig.nl/2025/04/rekenschema-normsterfte/
Das ist immer noch das lineare Modell.
Zahlen fĂŒr 2025 werden erst etwa im Juni 2026 verfĂŒgbar sein, CBS wird die ZĂ€hlung erst dann abgeschlossen haben.
Dass es im Jahr 2020 zu einer âgeplanten Stabilisierungâ unserer Gesundheit kommen wird, ist eine Annahme, die wir nicht getroffen haben. Wir gehen davon aus, dass das Sterblichkeitsrisiko von 2010 bis 2019 jedes Jahr um etwa 1 % sinkt. Das gibt uns nicht das GefĂŒhl, dass es ab 2020 plötzlich 0 % sein wĂŒrde, âweil es so lange gedauert hatâ. Die Gesundheitsversorgung kann unser Leben zunehmend verlĂ€ngern, insbesondere im Alter von 50 bis 60 Jahren, wie wir an den Zahlen sehen.
Im Gegensatz dazu sehen wir fĂŒr alle Jahre 2000-2008 einen RĂŒckgang von 2 % pro Jahr. Ein Nicken (schnelle Schritte in der Entwicklung von Behandlungsmethoden??). Aus diesem Grund beginnt unser Modell mit dem Jahr 2010, wĂ€hrend CBS nur 5 Jahre berĂŒcksichtigt, um einen Trend zu berechnen.
Und ja, aufgrund dieser Tatsache reagiert ein logarithmisches Modell gut auf diesen Knick und geht daher auch davon aus, dass diese Abflachung auch ab 2020 eintreten wird. Eine Wahl Ihres Modells geht ebenso wie eine Parabel davon aus, dass die Ăbersterblichkeit seit 2020 dadurch erklĂ€rt werden kann. Die Wahl Ihres Modells bestĂ€tigt, was Sie sehen möchten.
Und Unterschiede im Ergebnis Ihrer Berechnungen mĂŒssen auf die unbewussten Entscheidungen zurĂŒckzufĂŒhren sein, die Sie getroffen haben.
Na ja, eine freihĂ€ndige VerlĂ€ngerung der Trendlinie ist auch ârealistischâ oder logisch. Aber das ist etwas schwieriger zu berechnen, daher ist die exp()-Zeile, die exakte Punkte liefert, in Ordnung. Aber es bleibt âscheinbare Genauigkeitâ. Ich (oder Claude) werde am Ende 3 % höher sein als Sie. Also etwas weniger Ăbersterblichkeit.
Selbst dann weisen Frauen im Alter von 50 Jahren fĂŒr das Jahr 2024 immer noch eine deutliche Ăbersterblichkeit auf; und die MĂ€nner werden dann im Jahr 2024 innerhalb der Bandbreite liegen. Daher sind die Zahlen fĂŒr 2025 entscheidend, um zu sehen, wie es bei den MĂ€nnern (und natĂŒrlich auch bei den Frauen) weitergeht.
Ich hatte dieses Xcel vermisst; Danke; Ich werde sehen, ob ich die fehlenden Diagramme selbst erstellen kann. Obwohl ich im Moment sehr wenig Zeit habeâŠ.
Das Excel zeigt die Trendlinien fĂŒr alle Altersgruppen. Also alle Grafiken, die Sie im Kopf haben. Und erstellen Sie gerne Ihre eigenen Varianten, indem Sie Kohorten kombinieren.
Danke, ich werde es mir ansehen.
Und. NatĂŒrlich werde ich sie nicht kombinieren...
Das hĂ€ngt von der Frage ab. Wenn Sie beispielsweise wissen möchten, mit welcher Sterblichkeit Sie ĂŒber 65 Jahren rechnen, mĂŒssen Sie multiplizieren und addieren.
Nein, das interessiert mich nicht so sehr.
Ich bin nur neugierig auf die Ăbersterblichkeit pro Jahr und wie der Trend pro Jahr aussieht. Also etwa 80 (oder etwa 160 m/f) Diagramme mit etwa 20 Jahren (x-Achse) und TodesfĂ€llen/100.000 (y-Achse). Vielleicht kann ich ChatGPT dazu bringen, all diese Diagramme zu generieren ...
Noch 2 Details:
1. Ich verstehe nicht, warum der Logarithmus der âRealitĂ€tâ folgt und der Exponentialwert ĂŒberhaupt nicht. Mi. Bei Exponential kann man die 3 Parameter a · e^(bx) + c auch so wĂ€hlen, dass es bei einer glatten Kurve praktisch einer logarithmischen Kurve in der Reihe 2000 â 2019 entspricht. Auf jeden Fall viel besser, als Ihre Abbildung vermuten lĂ€sst!
2. Sie schreiben âLogarithmisch von 2000-2019. Ein Verlauf, der nicht durch einen physikalischen Hintergrund untermauert ist, aber wunderbar mit den Zahlen von 2003-2019 ĂŒbereinstimmt.â Ich denke, dass viele natĂŒrliche Prozesse eine logarithmische (asymptotenabnehmende, z. B. SĂ€ttigungseffekte, abnehmende ErtrĂ€ge, Lernkurven, Anpassung an neue Behandlungen, die einfachsten Verbesserungen werden zuerst erreicht, dann wird eine weitere Verbesserung zunehmend schwieriger) und/oder exponentielle (halber Wert, z. B. jede Verbesserung im Gesundheitswesen fĂŒhrt zu einer konstanten prozentualen Verbesserung) Abwanderung aufweist. Es ist also ĂŒberhaupt nicht so wunderbarâŠ.
ĂberprĂŒfen Sie noch einmal:
Claude landet mit exp() viel höher, nĂ€mlich 855/100.000 statt etwa 830/100.000 fĂŒr Sie. Das macht einen Unterschied von etwa 3 % und ist fĂŒr die Definition der Ăbersterblichkeit ziemlich viel. Oder hatten Sie eine ganz andere exp()-Funktion?
Rara?
Die log()-Funktion (hat nur 2 Parameter) passt nicht einfach durch 3 Punkte, aber ein ungefÀhrer log() ergibt ungefÀhr 830/100.000.
P.S. Claude findet eine gut passende Exp viel einfacher als eine Log-Funktion. Sie behaupten das Gegenteil.
Rara?
Exponentialfunktion
y = 516,204 Ă e^(-0,133482x) + 834,132
Prognose 2024
855.1
Logarithmische Funktion
y = 1360,342 + -166,417 Ă ln(x)
Prognose 2024
831,5
ĂberprĂŒfung: Passieren die Kurven die 3 Kontrollpunkte?
Jahr, tatsÀchliche Exp, vorhergesagter Exp-Fehler, Protokoll, vorhergesagter Log-Fehler
2003 1180 1180 0 1177,51 -2,49
2010 970 970 0 977,15 +7,15
2019 875 875 0 870,34 -4,66
Darin waren Herman und ich uns auch nicht ganz einig. Es bleibt eine Wahl fĂŒr einen beschreibenden Ansatz. Der demografische Ansatz bleibt der aussagekrĂ€ftigste PrĂ€diktor.
Ich persönlich verlasse mich beim Zeichnen von Trendlinien auf Excel. Daher weiĂ ich nicht genau, welche âBenchmarksâ Sie meinen, und auch nicht, warum diese Jahre Benchmarks sein sollten. Ich fĂŒge die gesamte Reihe in Excel ein, ich wĂ€hle keine Jahre aus, die meiner Meinung nach wichtiger sind (oder eine Linie besser unterstĂŒtzen) als andere. Dann ist das Ende wieder verloren.
The choice of segment is even decisive. Wenn man statt 2003 (oder 2002, das geht auch) das Jahr 2000 als Ausgangspunkt nimmt, dann stimmt das nicht mehr. Die Zeit vor 2000 ist wieder anders. Es bleibt eine Art Rosinenpickerei: Welches sieht am besten aus und könnte etwas Vorhersagendes zeigen? Welche Kristallkugel wird sich bald als richtig erweisen?
FĂŒr die Prognose macht die Wahl zwischen beiden (und sogar einer linearen) derzeit bei den Zehntausenden ungeklĂ€rten TodesfĂ€llen keinen groĂen Unterschied.
Vielleicht rechnet Claude etwas anders als Excel. DarĂŒber habe ich bereits mit ChatGPT gestritten, der sagt: Der Protokolltrend in Excel hat die Form: đŠ = đ ln(đ„) + đ
Ich hielt es fĂŒr selbstverstĂ€ndlich.
Im Jahr 2021 sprechen wir ĂŒbrigens nicht von einer âKnickungâ, sondern von einem unerwarteten Plateauanstieg, einem Trendausbruch aus dem Nichts, der sofort abflacht und langsam, hoffentlich dauerhaft, zurĂŒckfĂ€llt.
Erfreulicherweise ist ein langsamer AbwĂ€rtstrend erkennbar, wenngleich die Jahre 2024â2025 immer noch höher endeten als 2023â2024. Den Fokus auf 2024 finde ich nicht besonders interessant. In jedem Fall wĂ€re es viel besser, die Saisonjahre zu betrachten, aber dann wĂ€re man auch wieder auf dem falschen Weg. Man hĂ€tte gehofft, dass es nach 2021-2022 â oder eigentlich: direkt nach der Impfung â vorbei wĂ€re. Immerhin wurde das versprochen. Es bleibt abzuwarten, was 2025â2026, insbesondere diesen Winter, bringen wird.
Was meinen Sie mit demografischem vs. deskriptivem Ansatz?
FĂŒr einen Vergleich mit 3 Unbekannten benötigt man 3 Benchmarks. Ich habe die Extremwerte der Grafik genommen und eines etwa in der Mitte, also 2003, 2010 und 2019. Bei dieser Wahl sollte man keine AusreiĂer nehmen, sondern Punkte, die möglichst nahe an der Mitte der Linie liegen. Und das war 2010. Daher.
Ich bin nicht der Meinung, dass linear das Gleiche bewirkt. Das macht wirklich einen groĂen Unterschied, wie Sie in meinem vorherigen Beitrag sehen können. Es gibt also eine bessere Passform mit einer exp()-Funktion als die, die Xcel fĂŒr Sie berechnet: die von Claude. Aber Sie haben Recht: Es bleibt eine Extrapolation in die Zukunft, und Sie blicken also auf Kaffeesatz.
Im Jahr 2020 und darĂŒber hinaus wird es sicherlich zu einer deutlichen Abweichung vom bisherigen Trend kommen. Ich meinte, dass es im Jahr 2019 einen Wendepunkt geben könnte (genau wie um 2010 herum), ab dem die Lebenserwartung ohnehin weniger schnell steigen wĂŒrde. Auch das ist und bleibt Spekulation. Niemand hat dort ein Monopol auf die Wahrheit. Und aufgrund der Störungen durch Corona (und der âgroĂen Unbekanntenâ) werden wir leider nie erfahren, was ohne diese Störungen passiert wĂ€re ...
Auch Bonnes Jahreszeiten fand ich sehr aufschlussreich. Dagegen gibt es nicht viel zu sagen...
Wir ziehen keine Linie durch 3 Punkte, sondern 200 Linien durch 20.000 Punkte und ein Produkt aus 200 Linien mit 20.000 Einwohnerzahlen pro Jahr.
Demographisch: Vorhersehbare Bevölkerungsstruktur wird berĂŒcksichtigt
Beschreibend: Eine Formel, die ungefÀhr beschreibt, wie ein Muster (normalerweise eine Linie) von Ergebnissen verlÀuft.
Und wenn der Verlauf der Kurve fast vollstĂ€ndig von der Demografie bestimmt wird, muss man ihn nicht mehr beschreiben, denn diese Zahlen sind bereits bekannt ... đ
Wenn ein Zeitraum mit einer Formel beschrieben werden kann, ist er ein ernsthafter Kandidat fĂŒr die Vorhersage. Wenn die Vorhersagen nicht mit der Demografie ĂŒbereinstimmen, war es schön, dass es so lange gut lief đ
Mein Punkt ist, dass die Bevölkerungszusammensetzung genau bekannt ist. Sie werden keine Parabel âerfindenâ, um diesen Verlauf zu beschreiben. Sie mĂŒssen dies als gegeben in Ihr Modell einbeziehen. Was bleibt, ist ein Modell, das nur Ihre gesundheitliche Entwicklung widerspiegelt.
Sollte die Prognose gut ĂŒbereinstimmen, ist dies kein Beweis dafĂŒr, dass das Modell korrekt ist.
Schöner Artikel mit hervorragenden Grafiken, den ich auch verwenden werde. Meiner Meinung nach geht es vor allem darum, durch die Wimpern sehen zu können und nicht darum, daraus weitere spekulative Erkenntnisse abzuleiten. Dies ist nĂŒtzlich, um den Anstieg der Sterblichkeit von einer alternden Bevölkerung zu trennen, bei der es sich nicht um einen Turboanstieg handeln kann.
Bekanntlich streben wir beim Biomedizinischen Rechnungshof weiterhin nach mehr Transparenz der Zahlen. Bei RIVM. Bei CBS. Es wurden zwar Rohdaten zu den Todesursachen eingegeben, CBS erklĂ€rte sich jedoch aufgrund des CBS Act fĂŒr unzulĂ€ssig. Angesichts dieser Rechtsauffassung muss eine politische Lösung in Form einer GesetzesĂ€nderung gefunden werden. Zumindest wenn gute RegierungsfĂŒhrung das Ziel ist. Und was VWS/RIVM betrifft, warten wir immer noch auf die höhere Berufung im Deltavax-Fall! Staatsrat, machen Sie mit der Planung weiter, wĂŒrde ich sagen.
Und wir arbeiten auch mit einem Schwerpunkt hauptsĂ€chlich auf der Pathologie. Alle Erkenntnisse mĂŒssen mit kausalen medizinischen Beobachtungen verknĂŒpft werden. DarĂŒber ist bereits viel bekannt, obwohl die Forschung aktiv unterdrĂŒckt und entmutigt wird. Und bald folgt noch mehr darĂŒber, wie viel Sand in die Gesundheitsmaschine geworfen wurde und wie dieser erkannt werden kann. Mit schwerwiegenden Folgen fĂŒr die MortalitĂ€t, aber auch fĂŒr die MorbiditĂ€t. Bleiben Sie dran!
Hallo Cyril, danke!
Ich verfolge die gute Arbeit des BMRK aufmerksam. Ich habe in letzter Zeit wieder darauf geachtet, genau wie Sie hier Du hast es vielleicht gesehen.
Kausale medizinische Beobachtungen liegen sicherlich bereits vor. Alles hĂ€ngt davon ab, wie die Medien damit umgehen. Bisher gab es kaum Interesse daran. Die GrĂŒnde liegen auf der Hand.
Datentransparenz ist entscheidend; Meiner Meinung nach sogar PrioritĂ€t 1, weil kausale Beobachtungen ohne numerische Auswirkungen leicht als anekdotisch, nicht bedeutsam oder sogar als Desinformation abgetan werden. Das sehen wir jetzt. Ich bin sehr gespannt, ob die Abgeordneten einer GesetzesĂ€nderung zustimmen werden â falls es jemals einen solchen Vorschlag gibt. Daumen drĂŒcken und weitermachen!
Lieber Cyril,
Vielen Dank fĂŒr Ihren positiven Kommentar. Wenn wir Ihre nĂŒtzlichen AktivitĂ€ten unterstĂŒtzen können, lassen Sie es uns bitte wissen!
AuĂerdem arbeite ich an einem Artikel zum Thema âeffektive Impfratenâ. Dadurch lĂ€sst sich die Wirksamkeit des Impfstoffs anhand der bekannten Zahlen gut einschĂ€tzen. Aus ZeitgrĂŒnden gibt es beim Schreiben jedoch keine groĂen Fortschritte.
Besonders nĂŒtzlich in den ersten Monaten der Impfung, wenn die Gruppe der Ungeimpften viel gröĂer ist als die der Ungeimpften. NĂŒtzlich im Hinterkopf behalten!
GrĂŒĂe, Herman
Wird Virusvaria zu einer nationalen Bedrohung?
Ich habe kĂŒrzlich eine automatische Datenschutzwarnung erhalten, als ich nach einer Website gesucht habe!
TatsÀchlich ist es gefÀhrlich, diese Seite zu besuchen.
Möglicherweise fangen Sie gerade an, an der vorgeschriebenen ErzÀhlung zu zweifeln.
Zeit fĂŒr eine NamensĂ€nderung? âAusgezeichnetâ kommt mir in den Sinn. Excel, Transplantation (mehrere Bedeutungen), Impfung, ausgezeichnet... vielleicht habe ich zu viel Fantasie, aber leider habe ich auch Erfahrungen mit seltsamen Warnungen.