After 2021, the vaccinated in particular caused excess mortality

In this piece are previously found proportions in the United Kingdom applied to the Netherlands. No light cost but again a very urgent call for release of relevant data, so that independent and thorough research can be carried out so that we can work with solid material. But whichever way we look at it, there is no escaping vaccinations as a possible (co-)cause of excess mortality.

In recent weeks, we have calculated vaccine effectiveness for protection against Covid-19 and other causes of death in the UK for the period April 2021 – December 2022. This approach has now also been applied to the Dutch situation on the basis of the English figures.

For the Dutch situation, we look at the period July 2021 – December 2022. So we skip the first three months, the reason for this is that in the Netherlands the speed of vaccination was not that high in the beginning, so there was a lag behind the UK. This was later caught up, but the period up to July 2021 is therefore not usable to draw conclusions and has therefore been omitted from the calculations and graph for the Dutch situation.

The following steps have been completed:

1. The starting point is the mortality among unvaccinated English people per month;
2. Using data on vaccination coverage (defined as ever vaccinated) per day, it was calculated what mortality can then be expected per month among vaccinated people (under the assumption that vaccination does not affect mortality);
3. The expected mortality is compared with the actual observed mortality among vaccinated people. The quotient of actual mortality and expected mortality is called the factor Q (Q is therefore actual mortality divided by expected mortality).
   Calculation example: Suppose 600 unvaccinated people have died. After the groups have been made arithmetically the same size, the same mortality rate 540 vaccinated people had died, which is the expected number if both groups had been the same size. Then the simple division is: "540 divided by 600" and the result is 0.9. Lower than 1 therefore means: benefit for the vaccinated.
4. This results in a graph with the value of Q over time on the Y-axis. In England, we see that if we look at protection against Covid-19 as a cause of death, Q is below one over time, with an upward trend (2021 around 0.2 – 2022 around 0.8). However, if we look at all the causes of death, we see a line that soon rises above one and peaks in 2022 and more or less stabilizes around 1.40. This means that for every 10 deaths in the unvaccinated group, we see 14 in the vaccinated portion per the same group size.

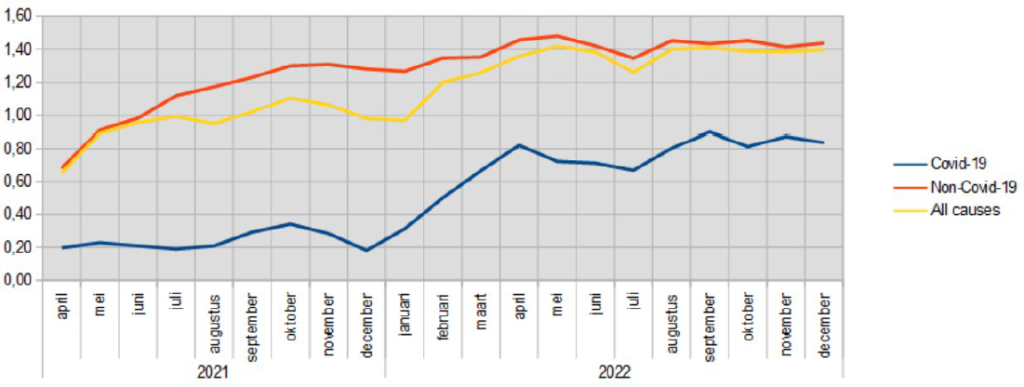
If the vaccine has no effect, then the value of Q is equal to one. If it has a positive effect, then the value of Q is less than one. The closer to zero the better. However, if Q is greater than one, the vaccine has a negative effect. This picture comes from an analysis of the data from the UK. For the Netherlands, as explained above, we will look from July 2021.

The analysis is now complemented by:

5. It is assumed that the course of Q in the Netherlands is similar to that in England. With this course we can determine what can be a possible distribution of vaccinated or unvaccinated deaths in the Netherlands.
6. To this end, we still have to take into account the lower vaccination rate in the Netherlands. It is believed to be 90% of the vaccination rate in England. A lower vaccination rate means that the numbers of unvaccinated deaths will rise and the actual and expected numbers of vaccinated deaths will decrease.
7. We must also correct for the fact that the English population is more than three times as large as the Dutch population and there are also demographic differences. We did this by comparing the mortality per month and total for the entire period for both countries.

In this comparison, we only look at "all cause mortality" (all causes of death combined). First of all, let's look at the mortality rates of the two groups. From July 2021 to January 2022, they hardly seem to avoid each other. From February 2022, they will diverge sharply, as the following figure shows:

You will also get these percentages if you assume 0% vaccinated (for Unvaccinated) and 100% vaccinated (for Vaccinated). Now we can also calculate what the mortality rates would be with an arbitrary vaccination rate. In the following figure these are added for 20% / 40% / 60% / 80%:

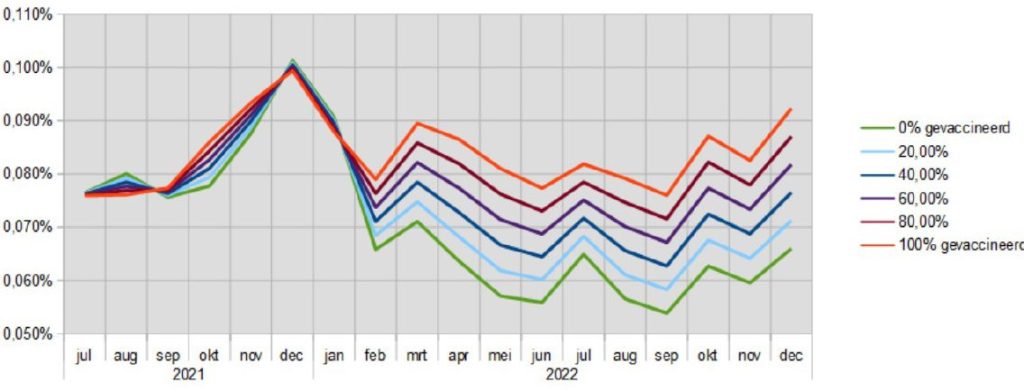
What we're seeing is that the higher the vaccination rate, the higher the death rates are, particularly in 2022. Now, of course, the question comes into play: does a higher vaccination rate also result in excess mortality?

To what extent is vaccination coverage a factor in excess mortality?

Let's expand the graph above with the expected mortality in the period July 2021 – December 2022. For clarity, the lines from the figure above have been pushed back a bit:

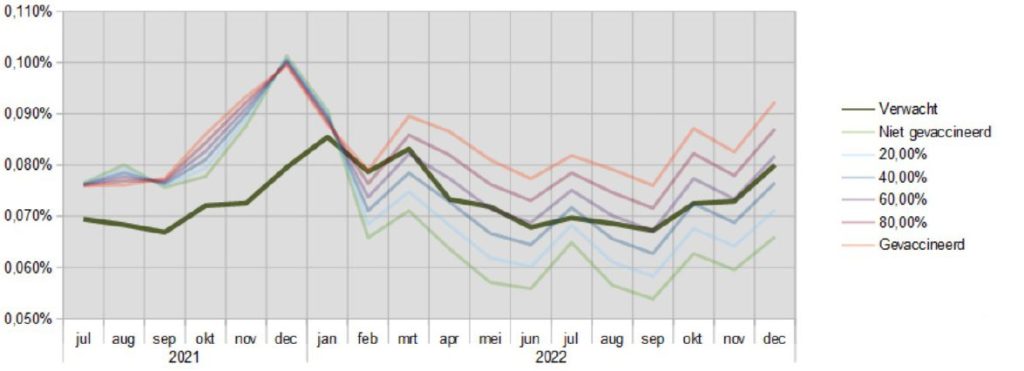
The expected mortality appears to be lower than any other line until January 2022. This implies that in this period the vaccination rate is not a (major) factor in the occurrence of excess mortality. However, how different it is in 2022. From February to December 2022, the expected mortality is somewhere in the middle of the other lines. This implies that if the vaccination rate had been around 50%, this situation would have led to less or no excess mortality in 2022.

We know that in the Netherlands the vaccination rate for 18+ is around 80%. This means that we expect the actual mortality rates to be close to the 80% line in 2022. The following figure also shows this:

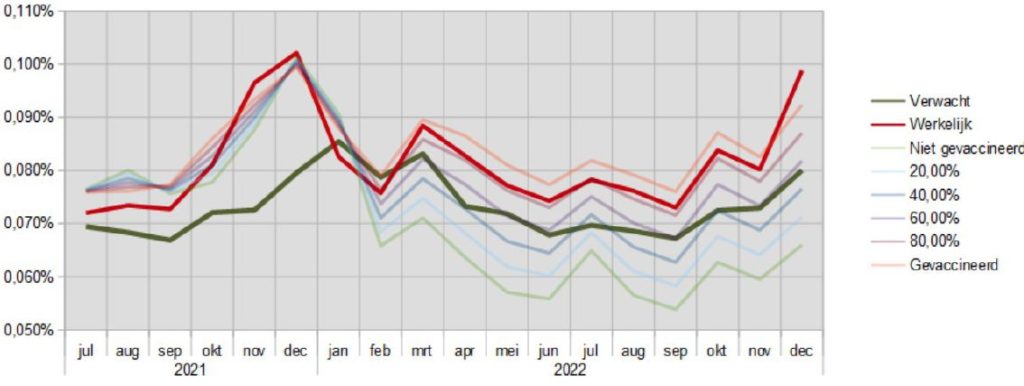
The figure above clearly shows that the actual mortality rates in 2022 are always close to the 80% vaccinated line. Often even slightly above it. For 2021, the actual mortality is always close, sometimes above it, sometimes below it at all lines.
From July 2021 until the end of the year, excess mortality in the Netherlands amounted to approximately 12,000 people. Over the whole of 2022, this was 14,000 people.

Conclusions

• In 2021, both vaccinated and unvaccinated will make a proportionate contribution to excess mortality.
• In 2022, the vaccinated in particular contributed to excess mortality.

Discussion

To what extent is this a true representation of reality? There are many uncertainties:

• Are the data from the UK correct?
• The Netherlands is a different country with a different population composition and vaccination rate. The correction to this may be subject to improvement.
• The moments of vaccination / boosters were not synchronised between the two countries, although this has also been taken into account.
• Is the course of corona and/or flu waves similar in both countries?

In theory, things could look very different in the Netherlands, but we know that corona caused fewer deaths in 2022 than in 2021, while excess mortality was higher in 2022 (and over a much longer period, almost three-quarters of a year). Perhaps another explanation is possible, but it has not yet reached me.

So it certainly makes sense to take a good look at the vaccination status of deceased people in the Netherlands and draw conclusions from that.